每日一题:多边形三角剖分的最低得分

2025/9/29 每日一题算法

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形剖分为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。

示例 1：

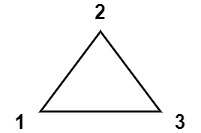
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

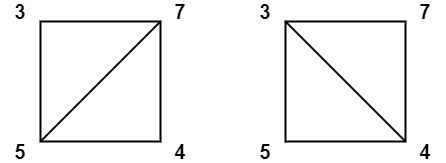
输入：values = [3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

示例 3：

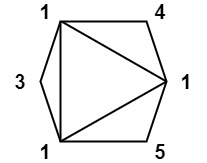
输入：values = [1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

提示：

n == values.length
3 <= n <= 50
1 <= values[i] <= 100

这种问题看似复杂，其实是找规律，利用递归的思路。重要的两个点在于多边形和三角形。一个多边形可以划分成多个三角形，而一个三角形主要是一条边加一个顶点。也就是说，需要固定一条边，然后枚举找顶点。多边形可以继续划分多边形和三角形，这就构成一个子问题。

以一个五边形举例，就是可以固定两个点作为找的三角形的底边，然后枚举顶点。找到一个顶点可以构成一个三角形，而这个三角形的左右两边也有多边形（即子问题）。这个五边形的答案就是左右子问题加中间三角形，找最小值就是题目答案。

书面一点的解释就是区间DP

定义状态： DP[i][j] 为从顶点 i 到 j的子多边形剖分的最小得分。

基准情况： 长度为 2 的区间 (DP[i][i+1]) 对应于多边形的一条边，不能构成三角形，所以 DP[i][i+1] = 0。

遍历区间长度： 从 len=3（三角形）开始递增，确保计算子问题时，其解 DP[i][k] 和 DP[k][j] 已经求得。

状态转移：对于每个 DP[i][j]，枚举分割点 k（i<k<j），将大问题分解为△(i,k,j)和两个子问题（左右多边形）。

$\text{Score}(i, j) = \min_{k} { v_i \cdot v_k \cdot v_j + DP[i][k] + DP[k][j] }$

以下是参考代码：

public class Solution {
    public int MinScoreTriangulation(int[] values) {
        int n = values.Length;
        int[,] dp = new int[n, n];

        for (int len = 3; len <= n; len++) {
            for (int i = 0; i <= n - len; i++) {
                int j = i + len - 1;
                dp[i, j] = int.MaxValue;
                for (int k = i + 1; k < j; k++) {
                    dp[i, j] = Math.Min(dp[i, j], dp[i, k] + dp[k, j] + values[i] * values[k] * values[j]);
                }
            }
        }

        return dp[0, n - 1];
    }
}

LOADING

每日一题:多边形三角剖分的最低得分