【题目指路】每日一题:最大三角形面积
给你一个由 X-Y 平面上的点组成的数组 points ,其中 points[i] = [xi, yi] 。从其中取任意三个不同的点组成三角形,返回能组成的最大三角形的面积。与真实值误差在 10^-5 内的答案将会视为正确答案。
示例 1:
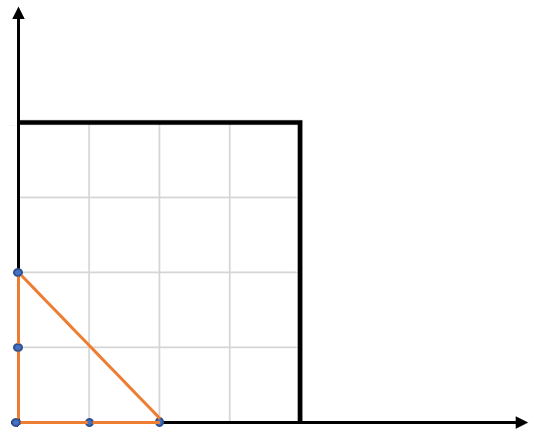
输入:points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出:2.00000
解释:输入中的 5 个点如上图所示,红色的三角形面积最大。
示例 2:
输入:points = [[1,0],[0,0],[0,1]]
输出:0.50000
提示:
3 <= points.length <= 50-50 <= xi, yi <= 50- 给出的所有点 互不相同
题目的意思很清晰,就是要找能构成最大三角形面积的三个点。最直接的方法自然是暴力枚举,三重循环枚举三个点。有三个点坐标就可以直接算三角形的面积了,然后比较获取最大值。计算方法可以用初中学过的海伦公式,高中的向量叉积或者向量点积和三角函数。这里以向量叉积为例子写代码。
public class Solution {
public double LargestTriangleArea(int[][] points) {
int n = points.Length;
int ans = 0;
for(int i = 0; i < n - 2; i++){
for(int j = i + 1; j < n - 1; j++){
for(int k = j + 1; k < n; k++){
int x1 = points[j][0] - points[i][0];
int y1 = points[j][1] - points[i][1];
int x2 = points[k][0] - points[i][0];
int y2 = points[k][1] - points[i][1];
ans = Math.Max(ans,Math.Abs(x1 * y2 - x2 * y1));
}
}
}
return ans / 2.0;
}
}
海伦公式要开根号,三角函数要算角度,在计算机中都相对比较麻烦。向量叉积就只用乘除,相对比较友好。向量叉积的物理意义就是这个两条边构成的平行四边形的面积,三角形的面积就是这个面积的一半。如果高中知识没有全部遗忘的话,应该是比较容易理解这个的。
那么要怎么优化呢?
现在是要三重循环枚举三个点来进行计算。可以回到三角形面积的计算公式去思考,主要是要确定底和高,就可以计算。这就可以是两重循环,前提是能做到一个循环找底边,一个循环找高。问题是怎么快速确定底边呢?枚举显然是不行的。
看着思路有点不对 ,我们可以再想想这个问题本身。给出一组点,求构成三角形的最大面积。那是不是这个三角形的三个点应该都是在这个点图的最边缘。那就可以固定两个点,然后找第三个点。这里枚举两个点就行,第三个点不需要再通过循环查找。
整个的思路,我们可以像,在一个圆中,固定有一个直径,第三个点的移动对面积的影响是先增大后减小,即有一个峰值,是单调的。以i,j,k来代表三个点来讲,有单调性,枚举i,j,确定底边,然后找k,枚举j的时候,直接继续移动上次找到的k,不需要重新枚举k,当枚举完j的时候,k也已经同时找到了。而这个“圆”,在这个题目中,就是这个点图的最边缘点的集合,也就是点集的凸包。固定的直径就是三角形的底边,而找最高点就是找三角形的高。现在的核心问题就变成怎么求凸包了。只有先有这个凸包,才能满足前面提到的单调性。凸包是要最边缘的点的集合,显然可以先排序。可以按照点的坐标从X优先后Y进行排序,就可以将这些点拟合成近似一条线。但是接下来要怎么操作?思考到这里我就不会了,遂询问ai得出,凸包可以使用单调链,前面那个找面积的方法有个名词叫旋转卡壳。具体代码如下
public class Solution {
public double LargestTriangleArea(int[][] points) {
// 1. 先求凸包
List<int[]> hull = ConvexHull(points);
int h = hull.Count;
if (h < 3) return 0.0;
double maxArea = 0.0;
// 2. 旋转卡壳求最大三角形面积
for (int i = 0; i < h; i++) {
for (int j = i + 1; j < h; j++) {
int k = (j + 1) % h;
// 移动 k,找到使面积最大的点
while (true) {
double curArea = Area(hull[i], hull[j], hull[k]);
double nextArea = Area(hull[i], hull[j], hull[(k + 1) % h]);
if (nextArea > curArea) {
k = (k + 1) % h;
} else {
maxArea = Math.Max(maxArea, curArea);
break;
}
}
}
}
return maxArea;
}
// 计算三角形面积(叉积公式)
private double Area(int[] a, int[] b, int[] c) {
long x1 = b[0] - a[0];
long y1 = b[1] - a[1];
long x2 = c[0] - a[0];
long y2 = c[1] - a[1];
return Math.Abs(x1 * y2 - x2 * y1) / 2.0;
}
// 凸包(Andrew 单调链算法)
private List<int[]> ConvexHull(int[][] points) {
Array.Sort(points, (p1, p2) => {
if (p1[0] == p2[0]) return p1[1].CompareTo(p2[1]);
return p1[0].CompareTo(p2[0]);
});
List<int[]> lower = new List<int[]>();
foreach (var p in points) {
while (lower.Count >= 2 && Cross(lower[lower.Count - 2], lower[lower.Count - 1], p) <= 0) {
lower.RemoveAt(lower.Count - 1);
}
lower.Add(p);
}
List<int[]> upper = new List<int[]>();
for (int i = points.Length - 1; i >= 0; i--) {
var p = points[i];
while (upper.Count >= 2 && Cross(upper[upper.Count - 2], upper[upper.Count - 1], p) <= 0) {
upper.RemoveAt(upper.Count - 1);
}
upper.Add(p);
}
lower.RemoveAt(lower.Count - 1);
upper.RemoveAt(upper.Count - 1);
lower.AddRange(upper);
return lower;
}
// 叉积判断 (b - a) × (c - a)
private long Cross(int[] a, int[] b, int[] c) {
return (long)(b[0] - a[0]) * (c[1] - a[1]) - (long)(b[1] - a[1]) * (c[0] - a[0]);
}
}
