算法基础

算法学习的记录，以c++为示例

模板也是一步一步迭代更新

板子也不全是我自己原创的，应该站在巨人的肩膀上，因此，网络上我习惯用的板子也收集

我觉得比较好的内容都收集起来

【emmm，总感觉做成合集的话，好像不怎么适合观看，之后会以分块的形式，现在已经是合集的内容就不更改了，懒得删】

这里贴一个简单目录便于快速查看

目录

• 进制转换
• 高精度
• 二分
• 双指针
• 前缀和与差分
• STL
• 排序
• 快速幂
• 并查集
• 树与图
• DFS
• BFS
• 拓扑序
• 最短路
• 最小生成树
• 质数
• 组合计数
• 博弈
• 贪心
• 动态规划
• 手写堆
• kmp
• tire树
• 哈希表
• 线段树
• 树状数组
• ST表
• 欧拉函数
• 卷积
• 二分图
• 最近公共祖先(LCA)
• 2_SAT

时空复杂度分析

理论基础，做题的时候首先观察数据范围，确定解决方案的大致时间复杂度，再思考用什么数据结构，能用什么算法。

时间复杂度

大O,算法导论给出的解释：大O用来表示上界的，当用它作为算法的最坏情况运行时间的上界，就是对任意数据输入的运行时间的上界。

整体测试数据整理如下：

其中，递归算法的时间复杂度本质上是要看: 递归的次数 * 每次递归中的操作次数。

空间复杂度

空间复杂度是考虑程序运行时占用内存的大小，而不是可执行文件的大小。

其中，递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度

读入与输出

//scanf()和printf()较快
//cin和cout较慢
//加速cin和cout
#define ios {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);}
//在输入输出量大的时候，需要使用scanf()和printf()

二分

二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

二分法第一种写法

第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
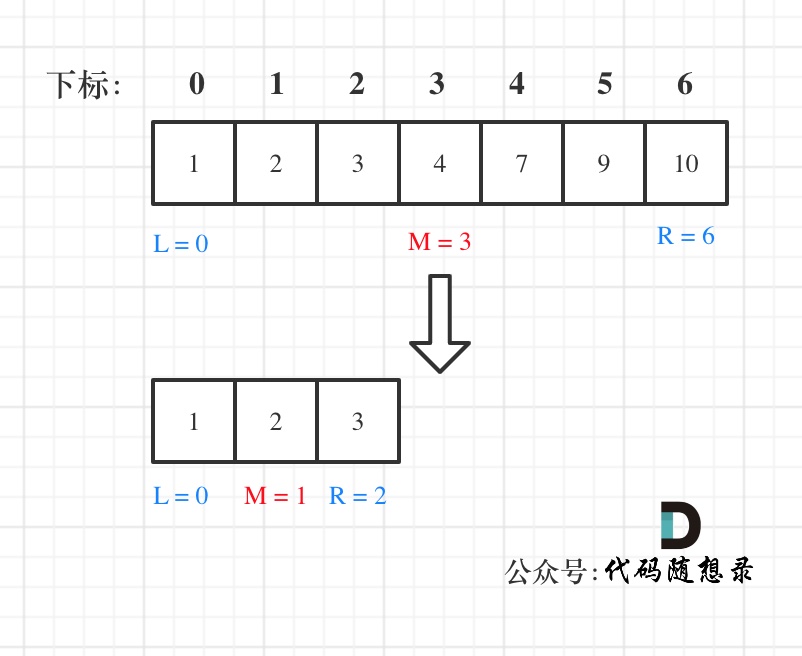
• if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：

代码如下：（详细注释）

// 版本一
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

• 时间复杂度：O(log n)
• 空间复杂度：O(1)

二分法第二种写法

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

有如下两点：

• while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
• if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）

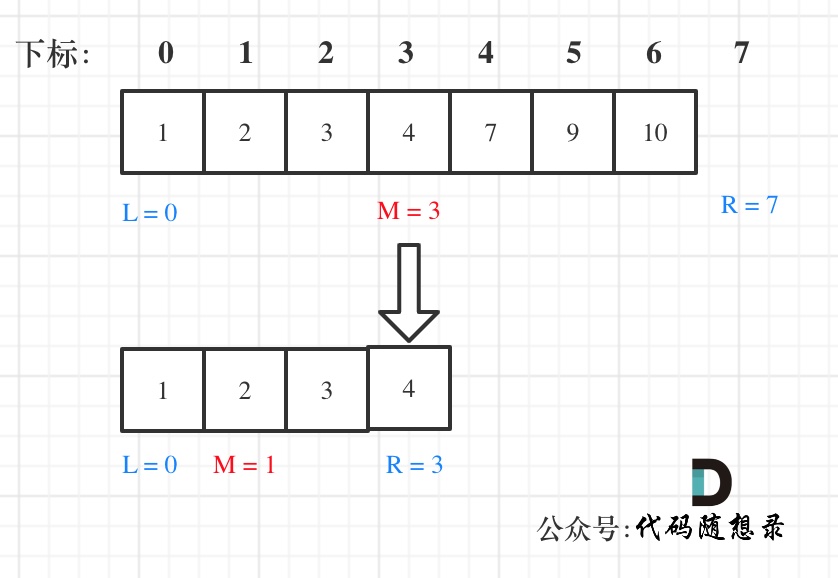
代码如下：（详细注释）

// 版本二
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

• 时间复杂度：O(log n)
• 空间复杂度：O(1)

二分查找

整数二分

bool check(int x)
{//检查x是否满足某种性质
    /*...*/
}

//区间[l,r]划分成[l,mid]和[mid+1,r]时
int bsearch_1(int l,int r)
{
    while(l<r)
    {
        int mid=l+r>>1;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    return l;
}
//区间[l,r]划分为[l,mid-1]和[mid,r]时
int bsearch_2(int l,int r)
{
    while(l<r)
    {
        int mid=l+r>>1;
        if(check(mid)) l=mid;
        else r=mid-1;
    }
    return l;
}

//相较于上一个板子，我更喜欢这个板子
int find_max(vector<int> num,int q)
{//最大化查找
    int l=0,r=num.size();
    while(l+1<r)
    {
        int mid=l+r>>1;
        if(num[mid]<=q)
        {l=mid;}
        else
        {r=mid;}
    }
    return l;
}

int find_min(vector<int> num,int q)
{//最小化查找
    int l=0,r=num.size();
    while(l+1<r)
    {
        int mid=l+r>>1;
        if(num[mid]>=q)
        {r=mid;}
        else
        {l=mid;}
    }
    return r;
}

浮点数二分

bool check(double x)
{//检查x是否满足某种性质
    /*...*/
}

double bsearch_3(double l,double r)
{
    const double eps=1e-6;//eps表示精度，取决于题目对精度的要求
    while(r-l>eps)
    {
        double mid =(l+r)/2;
        if(check(mid)) r=mid;
        else l=mid;
    }
    return l;
}

二分答案

其实，二分答案就是二分查找加上check,关键在于check函数的题目要求，来找到答案

STL

常用库函数

排序

常用排序

利用stl的sort()函数

sort() 函数有 2 种用法，其语法格式分别为：

//对 [first, last) 区域内的元素做默认的升序排序
void sort (RandomAccessIterator first, RandomAccessIterator last);
//按照指定的 comp 排序规则，对 [first, last) 区域内的元素进行排序
void sort (RandomAccessIterator first, RandomAccessIterator last, Compare comp);

其中，first 和 last 都为随机访问迭代器，它们的组合 [first, last) 用来指定要排序的目标区域；另外在第 2 种格式中，comp 可以是 C++ STL 标准库提供的排序规则（比如 std::greater），也可以是自定义的排序规则。

使用sort对数组排序

#include<algorithm>

vector<int> v;
sort(v.begin(),v.end());

int a[N];
sort(a,a+n);

例子

使用 STL 标准库提供的排序规则

int main(){
    int arr[] = {2,6,3,5,4,8,1,0,9,10};
    sort(arr, arr+10, std::greater<int>());
    for(int i = 0;i < 10;i++)
        cout << arr[i] << " ";
    cout << endl;
    sort(arr, arr+10, std::less<int>());
    for(int i = 0;i < 10;i++)
        cout << arr[i] << " ";
}
// out
/*
10 9 8 6 5 4 3 2 1 0
0 1 2 3 4 5 6 8 9 10
*/

使用自定义比较器

bool cmp(const int a, const int b){
    return a < b;
}
int main(){
    int arr[] = {2,6,3,5,4,8,1,0,9,10};
    sort(arr, arr+10, cmp);
    for(int i = 0;i < 10;i++)
        cout << arr[i] << " ";
}
// out
/*
0 1 2 3 4 5 6 8 9 10
*/

使用 lambda 表达式自定义比较器

int main(){
    int arr[] = {2,6,3,5,4,8,1,0,9,10};
    sort(arr, arr+10, [](const int a, const int b){
         return a < b;
         });
    for(int i = 0;i < 10;i++)
        cout << arr[i] << " ";
}
// out
/*
0 1 2 3 4 5 6 8 9 10
*/

使用sort对map排序

map是用来存放<key, value>键值对的数据结构，可以很方便快速的根据key查到相应的value，map本身的实现方式内含了比较器的设置，只要我们在map初始化的时候传入比较器，即可完成对应的排序。

定义包含水果及其个数的map，按照水果名称字典序进行排序 （按key排序）

#include<map>

using namespace std;

int main(){
    map<string, int, less<string>> msi;
    msi["apple"] = 5;
    msi["watermelon"] = 2;
    msi["pear"] = 3;
    msi["peach"] = 6;
    msi["cherry"] = 10;

    for(auto item: msi)
        cout << item.first << " " << item.second << endl;

    return 0;
}
// out
/*
apple 5
cherry 10
peach 6
pear 3
watermelon 2
*/

定义包含水果及其个数的map，按照水果个数进行排序，当水果个数相同时，按照水果名称字典序排序 （将map转为vector进行排序）

bool cmp(const pair<string, int>& a, const pair<string, int>& b){
    if(a.second < b.second) return true;
    else if(a.second == b.second) return a.first < b.first;
    else return false;
}
int main(){
    map<string, int> msi;
    msi["apple"] = 5;
    msi["watermelon"] = 2;
    msi["pear"] = 3;
    msi["peach"] = 5;
    msi["cherry"] = 10;

    vector<pair<string, int>> vpi(msi.begin(), msi.end());
    sort(vpi.begin(), vpi.end(), cmp);

    for(auto item: vpi){
        cout << item.first << " " << item.second << endl;
    }

    return 0;
}
// out
/*
watermelon 2
pear 3
apple 5
peach 5
cherry 10
*/

O(nlogn)

快速排序

void quick_sort(int q[],int l,int r)
{
    if(l>=r) return;
    
    int i=l-1,j=r+1,x=q[l+r>>1];
    while(i<j)
    {
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i<j) swap(q[i],q[j]);
    }
    quick_sort(q,l,j),quick_sort(q,j+1,r);
}

归并排序

void merge_sort(int q[],int l,int r)
{
    if(l>=r) return;
    
    int mid = l+r>>1;
    merge_sort(q,l,mid);
    merge_sort(q,mid+1,r);
    
    int k=0,i=l,j=mid+1;
    while(i<=mid&&j<=r)
    {
        if(q[i]<q[j]) 
        {
            tmp[k++]=q[i++];
        }
        else
        {
            tmp[k++]=q[j++];
        }
        
    }
    
    while(i<=mid) tmp[k++]=q[i++];
    while(j<=r) tmp[k++]=q[j++];
    
    for(i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];
}

基于比较的排序(8个)

所有的不稳定都可以转化为稳定(按照数值顺序为首位,下标顺序为次位)

1.直接插入排序

做法:相当于每次把元素插入有序位置
时间复杂度

1.最好情况:整个数组都有序，只执行外层循环，O(n)
2.平均情况:O(n^2)
3.最坏情况:O(n^2)

辅助空间复杂度:O(1)

稳定

代码:

void insert_sort()
{
        //由于是从头往后做，前面做过的都是有序的，只需要找到合适位置，将后面整体往后移一位，在有序位置插入t
        for(int i=1;i<n;i++) //q[0]只有一个数，有序
        {
                int t=q[i],j=i;

                while(j&&q[j-1]>t)
                {
                        q[j]=q[j-1];
                        j--;
                }
                q[j]=t;
        }
}

2.折半插入排序

直接插入排序的不明显优化：用二分找到第一个>t的位置,优化了比较次数(O(n)->O(logn))，但是没有优化移动次数
时间复杂度

1.最好情况:整个数组都有序，只执行外层循环，里面都continue，O(n)
2.平均情况:O(n^2)
3.最坏情况:O(n^2)

辅助空间复杂度:O(1)

稳定

代码:

void binary_insert_sort()
{
        for(int i=1;i<n;i++)
        {
                int t=q[i];
                if(q[i]>=q[i-1]) continue;
                //二分出第一个>t的元素，将此之后的所有元素往后移动一位，再将t插到当前有序位置
                int l=0,r=i-1;
                while(l<r)
                {
                        int mid=l+r>>1;
                        if(q[mid]>t) r=mid;
                        else l=mid+1;
                }
                for(int j=i-1;j>=r;j--)
                        q[j+1]=q[j];
                q[r]=t;
        }
}

3.冒泡排序

做法:每次从后往前处理逆序对，把第i小的元素放i位，最多n-1次之后就有序，因为n-1次后，剩下的最后一个数一定是最大的
优化:可以通过交换次数进行优化，如果某一次没有交换一次，说明已经有序，直接break出去
时间复杂度

1.最好情况:整个数组都有序，第一次就break,O(n)
2.平均情况:O(n^2)
3.最坏情况:每次使逆序对-1，最坏有n^2个逆序对，O(n^2)

辅助空间复杂度:O(1)

稳定

代码:

void bubble_sort()
{
        for(int i=0;i<n-1;i++)//最多执行n-1次，n-1次后剩下的一个数一定是最大的
        {
                bool has_swap=false;//做优化，如果某次没有交换过一次，说明有序，直接break
                for(int j=n-1;j>i;j--)//前i个元素有序(0~i-1),只需要比较后面的，又因为每次比较j与j-1，所以j>i
                {
                        if(q[j]<q[j-1])
                        {
                                swap(q[j],q[j-1]);
                                has_swap=true;
                        }
                }
                if(!has_swap) break;
        }
}

4.(简单)选择排序——最朴素的做法，所以也最慢^+^

区别:冒泡排序可以看成是选择排序的优化
做法:选择排序不是处理逆序对，而是最朴素德每次找到第i小的元素，与第i位上的元素互换
时间复杂度

1.最好情况:O(n^2)
2.平均情况:O(n^2)
3.最坏情况:O(n^2)

辅助空间复杂度:O(1)

不稳定，如2(1) 2(2) 1,排序后1 2（2） 2（1)，相对位置发生了变化

代码:

void select_sort()
{
        for(int i=0;i<n-1;i++)//也是最多只需要n-1次，n-1次后剩下的一个元素就是最大的
        {
                int k=i;
                for(int j=i+1;j<n;j++)//前面i个有序(0~i-1),所以从i开始往后面找最小,进行交换
                        if(q[j]<q[k])
                                k=j;
                swap(q[i],q[k]);
        }
}

5.希尔排序——第一个把排序最坏时间复杂度降到O(n^2)之下的

做法:

1.每次把所有元素分组，每一组下标都是等差数列，公差d称之为增量，每组的公差d相同

2.每组内部做插入排序

3.以此类推，组内插入排序，不断细化公差d，直到为d为1

当d为n/2,n/4,n/8...,1时，时间复杂度最坏O(n^2)
当d为n/3,n/9,n/27,...,1时，时间复杂度O(n^(3/2))

原因:借助插入排序对于部分有序的序列排序效果好的特性进行优化

时间复杂度

根据d的划分来看的，种类多
大体上O(n(3/2))

辅助空间复杂度:O(1)

不稳定，因为会进行分组

代码:

void shell_sort()
{
        for(int d=n/2;d;d/=2)//枚举公差, for(int d=n/3;d;d==2?d=1:d/=3),并不是每一个都会除到1，所以要特判
        {
                for(int start=0;start<d;start++)//枚举起点，起点只会在1-d之间，对应下表就是0-d-1
                {
                        for(int i=start+d;i<n;i+=d)//枚举组内做插入排序，第一个元素有序,所以起点start+d
                        {
                                int t=q[i],j=i;
                                while(j>start&&q[j-d]>t)//起点位start
                                {
                                        q[j]=q[j-d];
                                        j-=d;//公差为d
                                }
                                q[j]=t;
                        }
                }
        }
}

6.快速排序(和归并排序一样，基于分治),且快排和哈希一般不考虑最坏情况时间复杂度

做法:1.找分界值通常x=q[l+r>>1] 2.用分界值把区间分为左右两端，使左<=x,x,x<=右 3.递归排序左右两段
这里与一些老教材不同，AcWing的模板不能保证排完序后中间那个数就是x，而一些老版的教材可以保证这一点

时间复杂度

1.最好情况:O(nlogn)
2.平均情况:O(nlogn)
3.最坏情况:O(n^2)

空间复杂度:由于需要调用系统栈，所以O(logn)

不稳定,因为在划分时，等于x的元素即可能在前，也可能在后
代码

void quick_sort(int q[],int l,int r)
{
        if(l>=r) return ;
        int i=l-1,j=r+1,x=q[l+r>>1];

        while(i<j)//双指针算法
        {
                do i++;while(q[i]<x);
                do j--;while(q[j]>x);
                if(i<j) swap(q[i],q[j]);
        }
        quick_sort(q,l,j),quick_sort(q,j+1,r);
        //递归的分界点，取j时,x不能为q[r],取q[l+r>>1];取i时，x不能取q[l],也不能取q[l+r>>1]，要取q[l+r+1>>1]
}

7.堆排序

down(i)

递归处理使以i为父节点的树满足大根堆/小根堆的定义方式，不满足就往下;满足就不变

删除堆顶操作

并不是真的delete，而是放到heap的size之外去
先于最后一个数heap[size]互换，再删除heap[size](就是size--，让我们索引不到，但实际还在数组中)
最后由于刚刚上来的数不一定是最值，所以需要down(1)使满足堆的递归定义

做法:

建立小根堆或大根堆

大根堆:每次删除堆顶（将堆顶删除,就是最后一个数替换堆顶），然后heap的size-1，表示不再管q[]中的最后一个数,最后记得down(1)，因为最后一个数不能保证是此时heap中最大的数

小根堆:可以每次先输出/用辅助函数存下来，再删除堆顶；或者和大根堆一样操作，然后逆序输出

时间复杂度

1.最好情况:O(nlogn)
2.平均情况:O(nlogn)
3.最坏情况:O(nlogn)

辅助空间复杂度:O(logn),因为要用递归

不稳定,第一个会与最后一个交换，相等就不稳定了

代码:

//可用大根堆，可用小根堆
void down(int u)
{
        int t=u;
        if(2*u<=sz && q[2*u]>q[t]) t=2*u;//用小根堆就改成<
        if(2*u+1<=sz && q[2*u+1]>q[t]) t=2*u+1;//用小根堆就改成<
        if(u!=t)
        {
                swap(q[u],q[t]);
                down(t);
        }
}
void heap_sort()
{
        sz=n;
        for(int i=n/2;i;i--)
                down(i);
        for(int i=0;i<n-1;i++)
        {
        //可以选择倒着输出q[]
        //也可以在删的时候输出小根堆的堆顶q[1]，由于只输出了n-1次,出循环后再输出q[1]就行
                swap(q[1],q[sz]);
                sz--;
                down(1);
        }

}

8.归并排序(基于分治)

做法:1.找分界点mid=(l+r)/2 2.用分界点把区间分为左右两端，递归处理这两段 3.二路归并

时间复杂度

1.最好情况:O(nlogn)
2.平均情况:O(nlogn)
3.最坏情况:O(nlogn)

空间复杂度:由于需要调用系统栈和辅助数组，所以O(logn+n) -> O(n)

稳定
代码

void merge_sort(int q[],int l,int r)
{
        if(l>=r) return ;

        int mid=l+r>>1;
        merge_sort(q,l,mid),merge_sort(q,mid+1,r);

        int k=0,i=l,j=mid+1;
        while(i<=mid&&j<=r)
        {
                if(q[i]<=q[j]) tmp[k++]=q[i++];
                else tmp[k++]=q[j++];
        }

        while(i<=mid) tmp[k++]=q[i++];
        while(j<=r) tmp[k++]=q[j++];

        for(i=l,j=0;i<=r;i++,j++)
                q[i]=tmp[j];
}

非比较排序

1.桶排序(又叫计数排序)

桶:实际上就是开数组，存储每个数值出现的次数，所以数组的大小取决于数值的大小
a[i]的位置取决于小于a[i]的数量+i左边等于a[i]的数量,所以可以想到用前缀和的思想来求位置

此时存在一个区别:有没有相等的数

1.如果所有数都不相等，可以直接从前往后做,位置为s[a[i]]-1
2.如果存在相等的数x，则需要从后往前摆放，s[x]-1,s[x]--,组合起来:--s[x]

这里s[x]-1是这么想的:假设第一个大于x的数为y,y的位置为s[x]
则最后一个x为s[x]-1,让后往前x的数量-1，所以s[x]--

思想:用桶+辅助数组直接把每个数摆放的应该放的位置，并保证相对位置不变
做法:为了保证相对顺序，倒着摆放

时间复杂度

1.最好情况:O(n+m)
2.平均情况:O(n+m)
3.最坏情况:O(n+m)

空间复杂度:由于要求统计数值的个数和求数值数量的前缀和，以及辅助数组，所以O(n+m)

稳定:倒着排保证的相对位置
代码

void bucket_sort()
{
        for(int i=0;i<n;i++)    s[q[i]]++;//记录数组中每个数值的数量
        for(int i=1;i<N;i++)    s[i]+=s[i-1];//对每个数的数量求前缀和
        //因为s[]的大小取决去桶的数量，也就是数组中数的大小
        for(int i=n-1;i>=0;i--) w[--s[q[i]]]=q[i];//避免相同的x相对位置乱序，倒着摆放，最后一个x的位置为s[x]-1，完事s[x]--
        //相当于位置为--s[x],所以就是w[--s[q[i]]]=q[i]
        for(int i=0;i<n;i++) q[i]=w[i];
}

2.基数排序

实际上就是一个多关键字排序，这个多关键字是把a[i]化为r进制的每一位(估计数值范围，范围内用什么进制都可以)

做法：

1.可以从高位递归到低位，需要用到系统栈;
2.可以从低位到高位枚举，由于桶排序是稳定的，所以基数排序也是稳定的

思想:用桶+辅助数组直接把每个数摆放的应该放的位置，并保证相对位置不变
做法:为了保证相对顺序，倒着摆放

时间复杂度

1.最好情况:O(k(n+r)),k为a[i]分为r进制的位数
2.平均情况:O(k(n+r)),k为a[i]分为r进制的位数
3.最坏情况:O(k(n+r)),k为a[i]分为r进制的位数

空间复杂度:由于要求统计数值的个数和求数值数量的前缀和，以及辅助数组，所以O(n+m)

稳定:从低到高做桶排序，每次高位都是以低位为基础，如果高位相同，则按照低位的相对位置排，所以稳定
代码

void radix_sort(int d,int r)//d表示关键字的位数,r表示r进制
{
        int radix=1;
        for(int i=1;i<=d;i++)//枚举每一位,从低位到高位,由于每次都是在上次的基础上再桶排序，所以稳定
        {
                for(int j=0;j<r;j++) s[j]=0;//可以直接用memset

                for(int j=0;j<n;j++) s[q[j]/radix%r]++;

                for(int j=1;j<r;j++) s[j]+=s[j-1];

                for(int j=n-1;j>=0;j--) w[--s[q[j]/radix%r]]=q[j];

                for(int j=0;j<n;j++) q[j]=w[j];
                radix*=r;

        }
}

外部排序(外存里的排序，主要取决于读取次数)

做法:

1. 置换选择排序(在内存中预处理出m个有序序列,m可能很大，大到内存存不下)
2. 再利用Huffman思想(每次去k个最短的序列)，使用败者树将k个序列合并成一个序列,k个序列归并
   所以读写时间复杂度为O(logk m)
3. 以此类推直到m个序列合并成1个序列

为了减少O(logk m)的读取时间复杂度，有两种方法

1. k增加，当时要权衡归并是内存对k的限制

2. m减小，用置换选择排序来生成更长的序列，从而使m减小

置换选择排序(内排序)主要有两种实现方法

1. 堆排序
拿小根堆为例
如当前序列读到x，此时堆顶为a
1.1 先输出a
1.2 if(x>a)
        插到堆顶，down(1)
    if(x<a) 
        不能放到堆顶,因为输出的序列要保持有序，直接插x到堆顶，下一次输出x会有a、x的序列，但是这是逆序的
        正确做法:把最后一个元素heap[size]放到堆顶，dowm(1),再将x放到最后元素的位置,up(size)
1.3 当堆为空时，就不能再操作，形成了一个升序序列，长度大概为2m
    再重新开文件做上述步骤，得到m个升序序列

2. 败者树(对胜者树排序的优化，优化IO次数) 

每次从m段有序序列中选k段，合并成一段，可以用Huffman树的思想来优化，相当于k进制的Huffman树
每合并k段，形成1段，所以每次减少k-1段，如果(m-1)%(k-1)!=0,则加0(也叫虚段)

k路归并时每次需要找到k个序列的最小值经行比较
可以用对来维护，而每次堆删除元素和插入比a更小的数，比较慢，删除——down(1),插入x(x<a)——down(1)+up(size)
所以可以将堆优化为胜者树

胜者树:结构是堆,但是从下往上建立

败者树:结构是堆，但是从下往上建立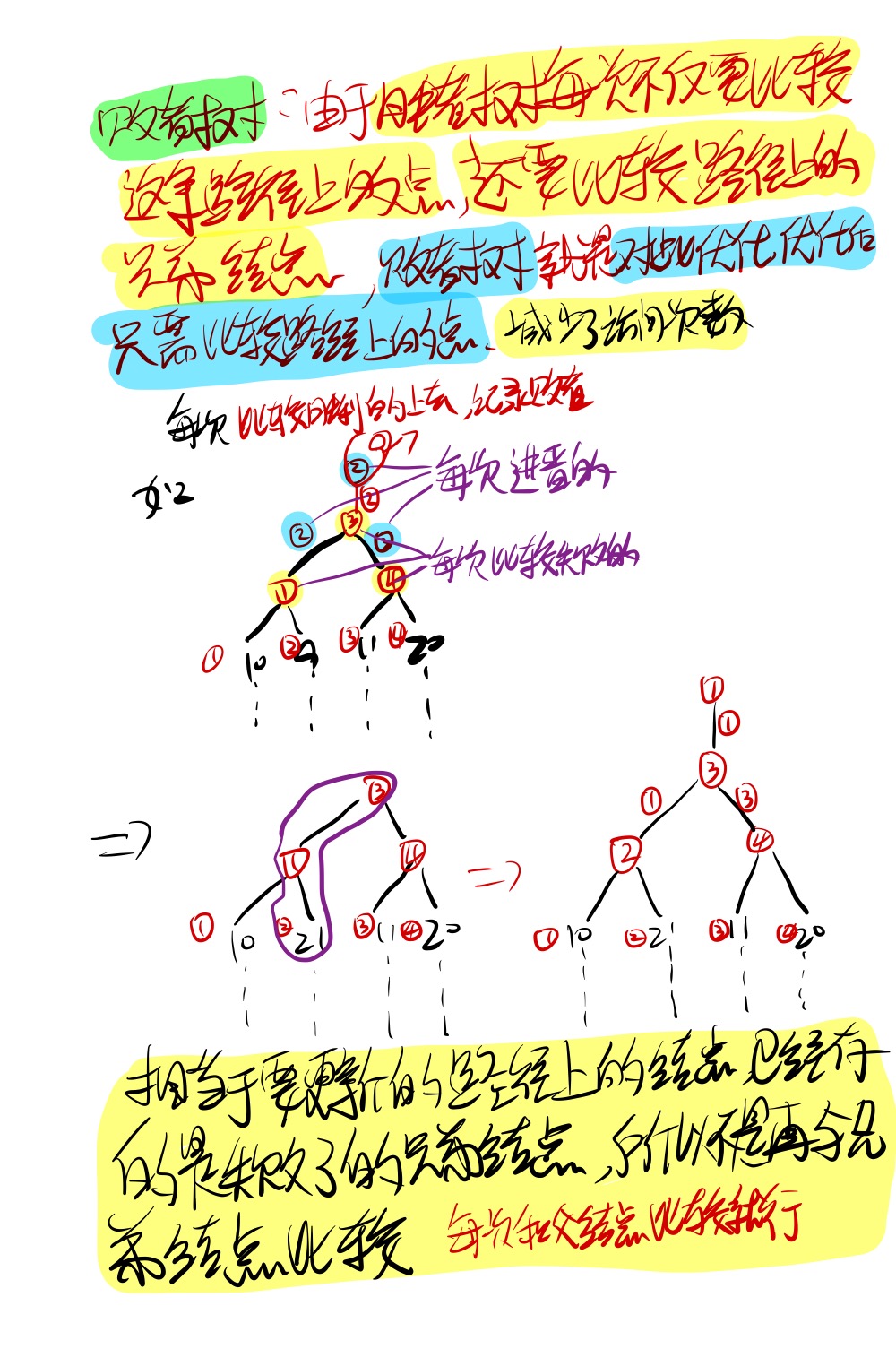

数据结构

数组（array）

数组是存放在连续内存空间上的相同类型数据的集合。

两点注意的是

• 数组下标都是从0开始的。
• 数组内存空间的地址是连续的

正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

数组的元素是不能删的，只能覆盖。

链表

链表是一种通过指针串联在一起的线性结构。算法竞赛中主要使用数组模拟链表。

单链表

每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。

链表的入口节点称为链表的头结点也就是head。指针域只能指向节点的下一个节点。

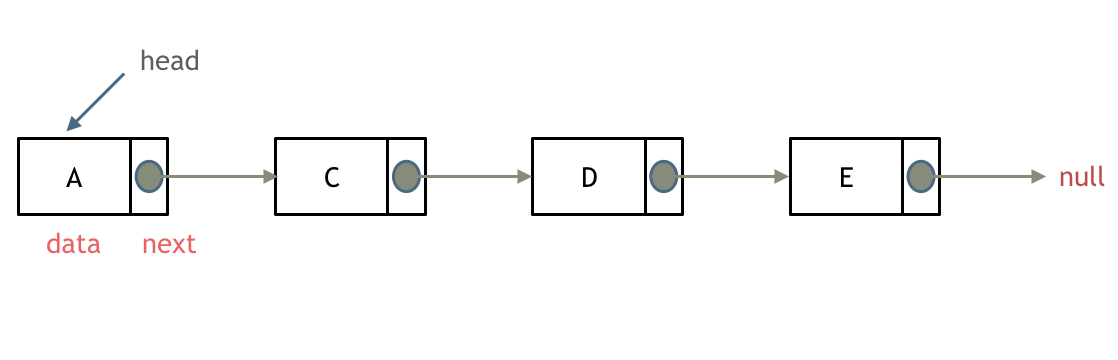
// 单链表
struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数
};

不定义构造函数行不行，答案是可以的，C++默认生成一个构造函数。

双链表

每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点。

双链表 既可以向前查询也可以向后查询。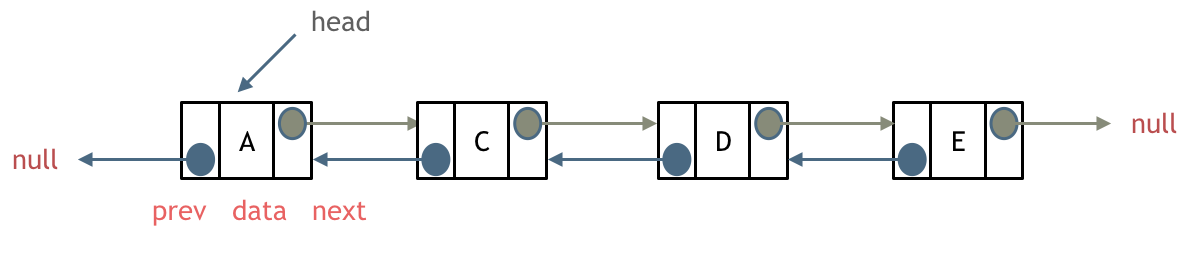

循环链表

循环链表，顾名思义，就是链表首尾相连。

数组模拟链表

单链表

//head存储链表头，e[]存储节点值，ne[]存储节点的next指针，idx表示当前索引用到了哪个节点
int head,e[N],ne[N],idx;

//初始化
void init()
{
    head=-1;
    idx=0;
}
//头插法
//在链表头插入一个数a
void insert(int a)
{
    e[idx]=a,ne[idx]=head,head=idx++;
}

//将x插到下标是k的点后面
void add(int k,int x)
{
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx++;
}

//将下标是k的点后面的点删掉
void remove(int k)
{
    ne[k]=ne[ne[k]];
}

//将头节点删除，需要保证头节点存在
void remove()
{
    head=ne[head];
}

双链表

//e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前索引用到了哪个节点
int e[N],l[N],r[N],idx;

//初始化
void init()
{
    //0是左端点，1是右端点
    r[0]=1,l[1]=0;
    idx=2;
}

//在节点a的右边插入一个数x
void insert(int a,int x)
{
    e[idx]=x;
    l[idx]=a,r[idx]=r[a];
    l[r[a]]=idx,r[a]=idx++;
}
//在节点a的左边插入一个数x可以调用右边插入的方法
insert(l[k],x);

//删除节点a
void remove(int a)
{
    l[r[a]]=l[a];
    r[l[a]]=r[a];
}

栈(stack)

STL中的栈

stack

size()//栈的大小
empty()//判断栈是否为空
push()//向栈顶插入一个元素
top()//返回栈顶元素
pop()//弹出栈顶元素

数组模拟栈

普通栈

//tt表示栈顶
int stk[N],tt=0;

//向栈顶插入一个数
stk[++tt]=x;

//从栈顶弹出一个数
tt--;

//栈顶的值
stk[tt];

//判断栈是否为空
if(tt>0)
{
    not empty
}

单调栈

常见模型：找出每个数左边离它最近的比它大/小的数

int tt=0;
for(int i=1;i<=n;i++)
{
    while(tt&&check(stk[tt],i)) tt--;
    stk[++tt]=i;
}

队列(queue)

STL中的队列

queue

size()
empty()
push()//向队尾插入一个元素
front()//返回队头元素
back()//返回队尾元素
pop()//弹出队头元素

priority_queue

优先队列，默认是大根堆

push()//插入一个元素
top()//返回堆顶元素
pop()//弹出堆顶元素    

定义成小根堆

priority_queue<int,vector<int>,greater<int>> q;

deque

双端队列

size()
empty()
clear()
front()/back()
push_back()/pop_back()
push_front()/pop_front()
begin()/end()
[]

数组模拟队列

普通队列

//hh表示队头，tt表示队尾
int q[N],hh=0,tt=-1;

//向队尾插入一个数
q[++tt]=x;

//从队头弹出一个数
hh++;

//队头的值
q[hh];

//队尾的值
q[tt];

//判断队列是否为空
if(hh<=tt)
{
    not empty
}

循环队列

//hh表示队头，tt表示队尾的后一个位置
int q[N],hh=0,tt=0;

//向队尾插入一个数
q[tt++]=x;
if(tt==N) tt=0;

//从队头弹出一个数
hh++;
if(hh==N) hh=0;

//队头的值
q[hh];

//判断队列是否为空
if(hh!=tt)
{
    
}

单调队列

常见模型：找出滑动窗口中的最大值/最小值

int hh=0,tt=-1;
for(int i=0;i<n;i++)
{
    while(hh<=tt&&check_out(q[hh])) hh++;//判断队头是否滑出窗口
    while(hh<=tt&&check(q[tt],i)) tt--;
    q[++tt]=i;
}

堆(heap)

手写堆的基本操作

1.插入一个数
    heap[++size]=x;up(size);
2.求集合中最小值
    heap[1]
3.删除最小值
    heap[1]=heap[size];size--;down(1);
4.删除任意元素
    heap[k]=heap[size];size--;down(k);up(k);
5.修改任意元素
    heap[k]=x;down(k);up(k);

手写堆的实现

//h[N]存储堆中的值，h[1]是堆顶，x的左儿子是2x,右儿子是2x+1
//ph[k]存储第k个的点是 第几个插入的
//hp[k]存储堆中下标是k的点是第几个插入的
int h[N],ph[N],hp[N],size;

//交换两个点及其映射关系
void heap_swap(int a,int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a],hp[b]);
    swap(h[a],h[b]);
}

void down(int u)
{
    int t=u;
    if(u*2<=size&&h[u*2]<h[t]) t=u*2;
    if(u*2+1<=size&&h[u*2+1]<h[t]) t=u*2+1;
    if(u!=t)
    {
        heap_swap(u,t);
        down(t);
    }
}

void up(int u)
{
    while(u/2&&h[u]<h[u/2])
    {
        heap_swap(u,u/2);
        u>>1;
    }
}

//O(n)建堆
for(int i=n/2;i;i--) down(i);

用stl库的priority_queue

字符串（string）

KMP

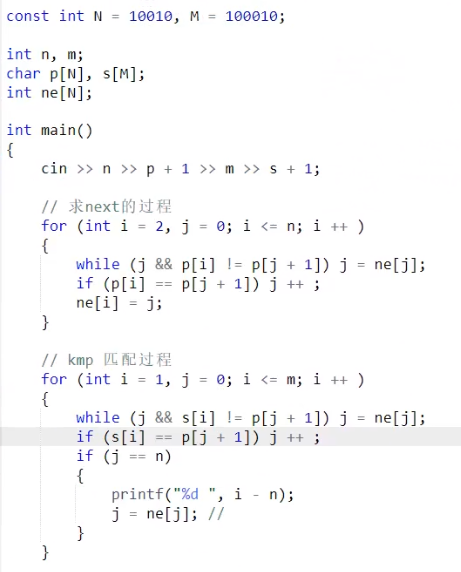
next[i]的值表示下标为i的字符前的字符串最长相等前后缀的长度。也表示该处字符不匹配时应该回溯到的字符的下标。

//求next数组
//s[]是模式串，p[]是模板串，n是s的长度，m是p的长度
for(int i=2,j=0;i<=m;i++)
{
    while(j&&p[i]!=p[j+1]) j=ne[j];
    if(p[i]==p[j+1]) j++;
    ne[i]=j;
}

//匹配
for(int i=1,j=0;i<=n;i++)
{
    while(j&&s[i]!=p[j+1]) j=ne[j];
    if(s[i]==p[j+1]) j++;
    if(j==m)
    {
        j=ne[j];
        //匹配成功后的逻辑
    }
}

exkmp(z函数)

tire树

int son[N][26],cnt[N],idx;
//son[][]存储树中每个节点的子节点
//cnt[]存储以每个节点结尾的单词数量
//0号点是根节点也是空节点

//插入一个字符串
void insert(char *str)
{
    int p=0;
    for(int i=0;str[i];i++)
    {
        int u=str[i]-'a';
        if(!son[p][u]) son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p++];
}

//查询字符串出现的次数
int query(char *str)
{
    int p=0;
    for(int i=0;str[i];i++)
    {
        int u=str[i]-'a';
        if(!son[p][u]) return 0;
        p=son[p][u];
    }
    return cnt[p];
}

最长回文子串

//中心扩展法

并查集

struct DSU {
    std::vector<int> f, siz;
    
    DSU() {}
    DSU(int n) {
        init(n);
    }
    
    void init(int n) {
        f.resize(n);
        std::iota(f.begin(), f.end(), 0);
        siz.assign(n, 1);
    }
    
    int find(int x) {
        while (x != f[x]) {
            x = f[x] = f[f[x]];
        }
        return x;
    }
    
    bool same(int x, int y) {
        return find(x) == find(y);
    }
    
    bool merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) {
            return false;
        }
        siz[x] += siz[y];
        f[y] = x;
        return true;
    }
    
    int size(int x) {
        return siz[find(x)];
    }
};

朴素并查集

int p[N];//存储每个点的祖宗节点

//返回x的祖宗节点
int find(int x)
{
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

//初始化，假定节点编号是1~n
for(int i=1;i<=n;i++) p[i]=i;

//合并a和b所在的两个集合
p[find(a)]=find(b);

维护size的并查集

int p[N],sz[N];//存储每个点的祖宗节点

//返回x的祖宗节点
int find(int x){
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

void init(int n){
    //初始化，假定节点编号是1~n
    for(int i=1;i<=n;i++){ 
        p[i]=i;
        sz[i]=1;
    }
}

void merge(int a,int b){
    int pa=find(a),pb=find(b);
    if (pa != pb) {
        if (sz[pa] < sz[pb]) {
            swap(pa, pb);
        }
        p[pb] = pa;
        sz[pa] += sz[pb];
    }
}

维护到祖宗节点距离的并查集

int p[N],d[N];
//p[]存储每个点的祖宗节点，d[x]存储x到p[x]的距离

//返回x的祖宗节点
int find(int x)
{
    if(p[x]!=x)
    {
        int u=find(p[x]);
        d[x]+=d[p[x]];
        p[x]=u;
    }
    return p[x];
}

//初始化，假定节点是1~n
for(int i=1;i<=n;i++)
{
    p[i]=i;
    d[i]=0;
}

//合并a和b所在的集合
p[find(a)]=find(b);
d[find(a)]=distance;//根据具体问题，初始化find(a)的偏移量

Hash表

哈希表是根据关键码的值而直接进行访问的数据结构。

一般哈希表都是用来快速判断一个元素是否出现集合里。

当我们想使用哈希法来解决问题的时候，我们一般会选择如下三种数据结构。

• 数组
• set （集合）
• map(映射)

一般哈希

拉链法

int h[N],e[N],ne[N],idx;

//向哈希表中插入一个数
void insert(int x)
{
    int k=(x%N+N)%N;
    e[idx]=x;
    ne[idx]=h[k];
    h[k]=idx++;
}

//在哈希表中查询某个数是否存在
bool find(int x)
{
    int k=(x%N+N)%N;
    for(int i=h[k];i!=-1;i=ne[i])
    {
        if(e[i]==x) return true;
    }
    return false;
}

开放寻址法

int h[N];

//如果x在哈希表中，返回x的下标；如果不在，返回x应该插入的位置
int find(int x)
{
    int t=(x%N+N)%N;
    while(h[t]！=null&&h[t]!=x)
    {
        t++;
        if(t==N) t=0;
    }
    return t;
}

字符串哈希

核心思想：将字符串看成P进制数，P的经验值是131或者13331，取这两个值的冲突概率低

小技巧：取模的数用2^64，这样直接用unsigned long long存储，溢出的结果就是取模的结果

typedef unsigned long long ULL;
ULL h[N],p[N];//h[k]存储字符串前k个字母的哈希值，p[k]存储 P^k mod 2^64

//初始化
p[0]=1;
for(int i=1;i<=n;i++)
{
    h[i]=h[i-1]*P+str[i];
    p[i]=p[i-1]*P;
}

//计算子串str[l,r]的哈希值
ULL get(int l,int r)
{
    return h[r]-h[l-1]*p[r-l+1];
}

二叉树

满二叉树

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

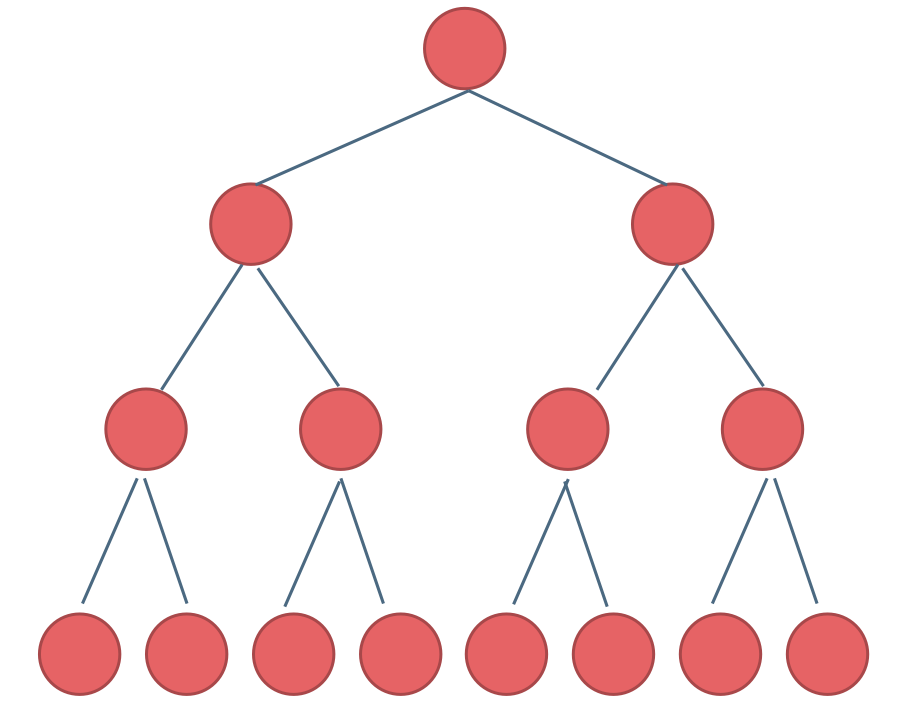
这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

完全二叉树

什么是完全二叉树？

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。

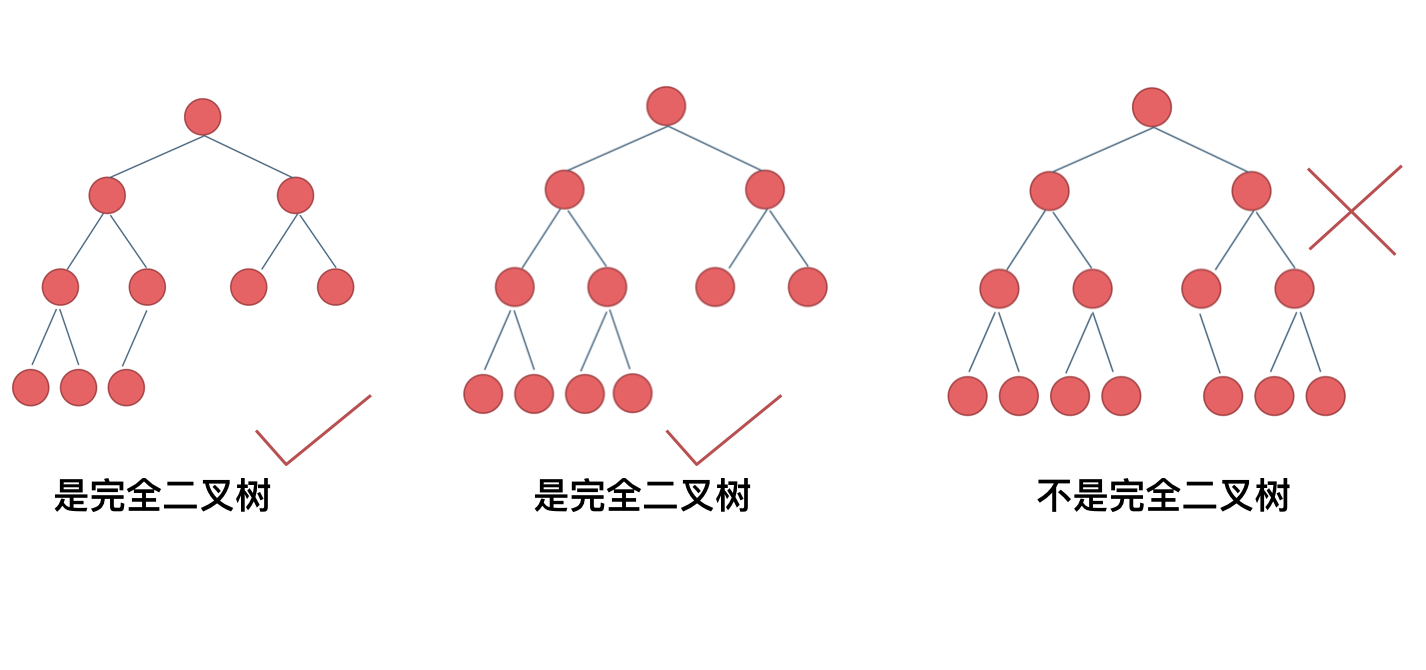
优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。

二叉搜索树

二叉搜索树是有数值的，二叉搜索树是一个有序树。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树

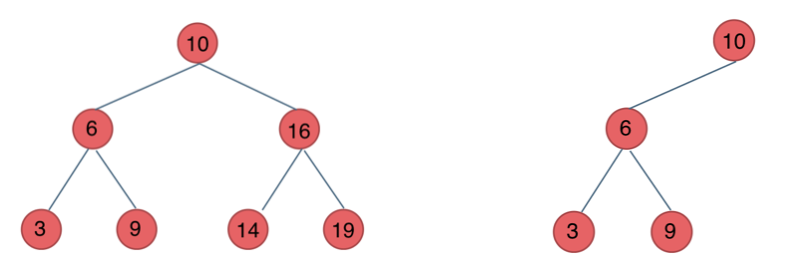
平衡二叉搜索树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

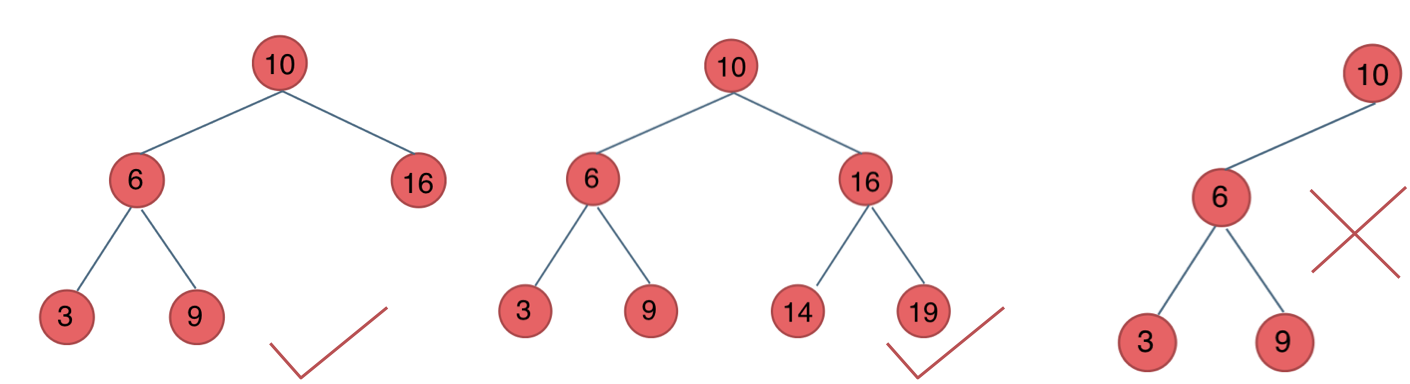
最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_set底层实现是哈希表。

二叉树的存储

二叉树可以链式存储，也可以顺序存储。

那么链式存储方式就用指针， 顺序存储的方式就是用数组。

顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在各个地址的节点串联一起。

链式存储如图：

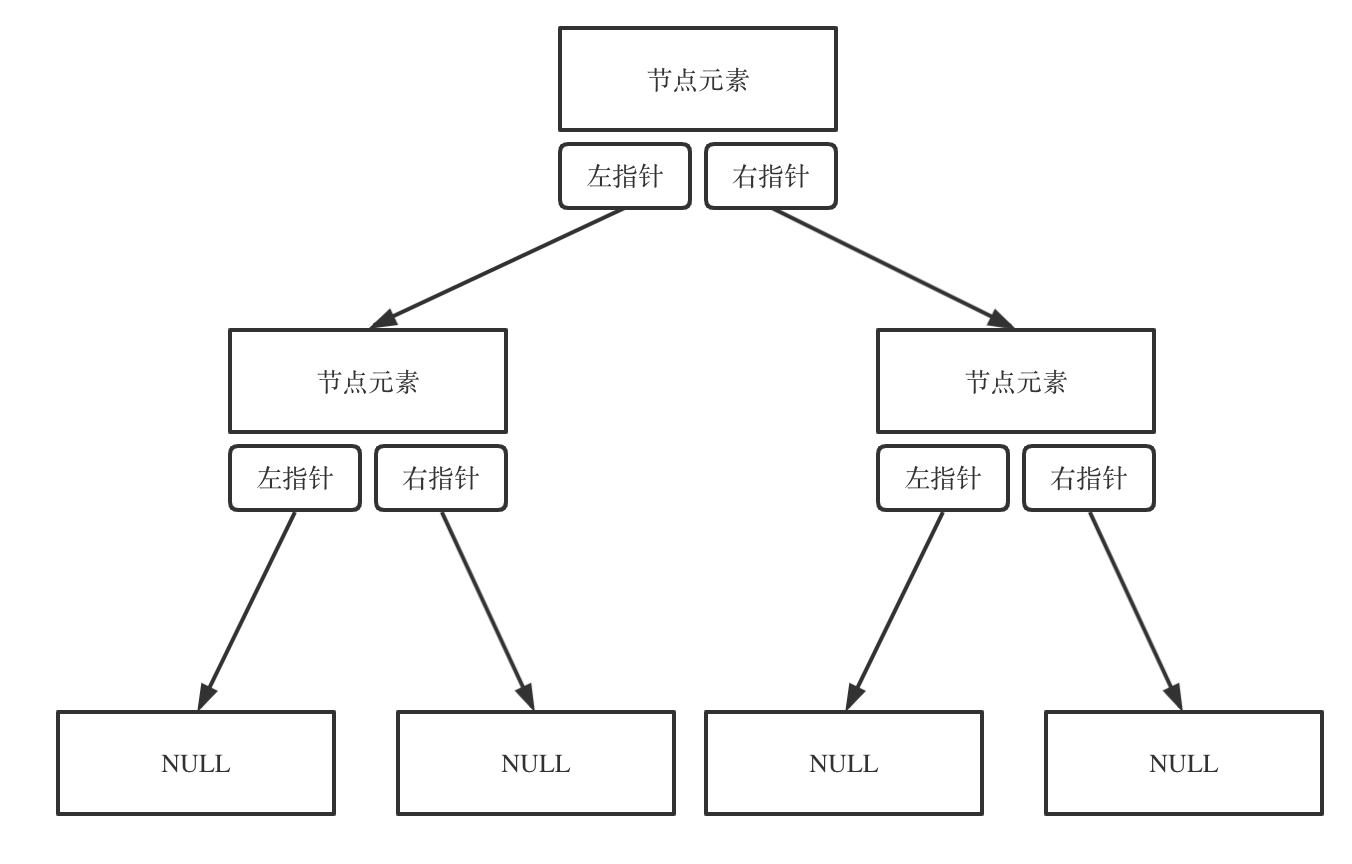
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

链式存储是大家很熟悉的一种方式，那么我们来看看如何顺序存储呢？

其实就是用数组来存储二叉树，顺序存储的方式如图：

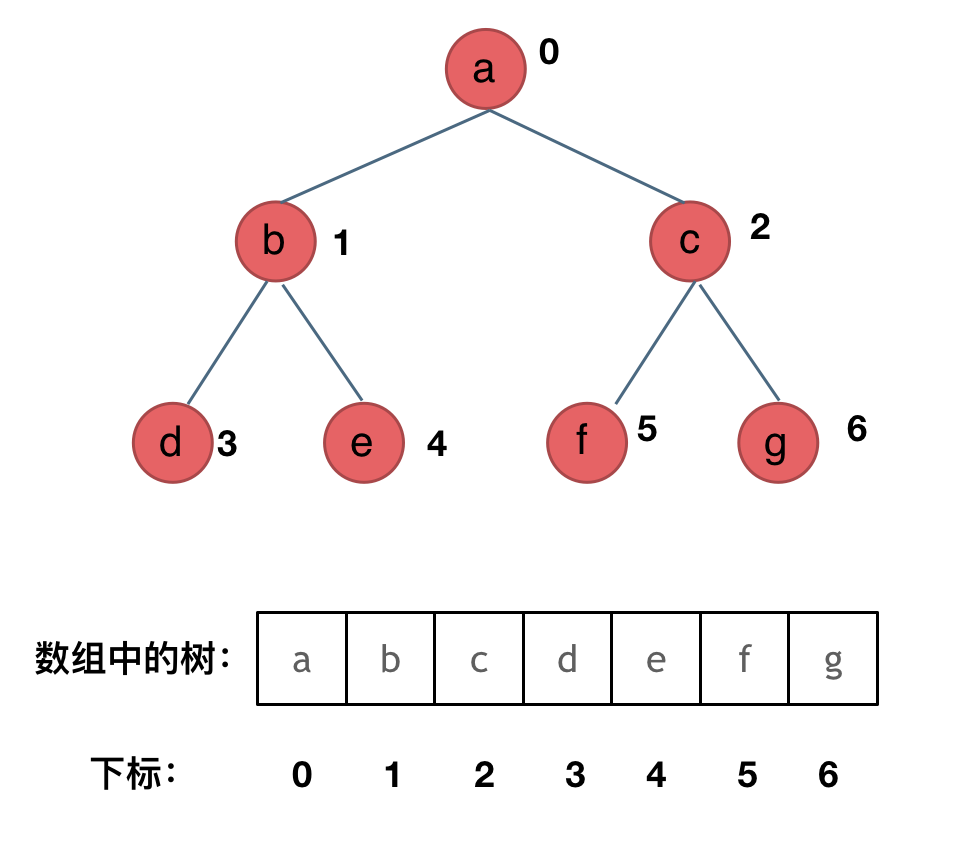
用数组来存储二叉树如何遍历的呢？

如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

//tree[N]存储堆中的值，tree[0]是根
tree[N];

线段树

区间取最小值更新和区间最小值查询

#define int long long
struct segmenttree
{
    int n;
    vector<int> st, lazy;

    void init(int _n)
    {
        this->n = _n;
        st.resize(4 * n, LLONG_MAX);
        lazy.resize(4 * n, LLONG_MAX);
    }

    void push(int start, int ending, int node)
    {
        if (lazy[node] != LLONG_MAX)
        {
            st[node] = min(lazy[node], st[node]);

            if (start != ending)
            {
                lazy[2 * node + 1] = min(lazy[2 * node + 1],lazy[node]);
                lazy[2 * node + 2] = min(lazy[node], lazy[2 * node + 1]);
            }

            lazy[node] = LLONG_MAX;
        }
    }

    int query(int start, int ending, int l, int r, int node)
    {
        push(start, ending, node);

        if (start > r || ending < l)
        {
            return LLONG_MAX;
        }

        if (start >= l && ending <= r)
        {
            return st[node];
        }

        int mid = (start + ending) / 2;

        int q1 = query(start, mid, l, r, 2 * node + 1);
        int q2 = query(mid + 1, ending, l, r, 2 * node + 2);

        return min(q1, q2);
    }

    void update(int start, int ending, int node, int l, int r, int value)
    {
        push(start, ending, node);

        if (start > r || ending < l)
        {
            return;
        }

        if (start >= l && ending <= r)
        {
            lazy[node] = min(lazy[node], value);
            push(start, ending, node);            
            return;
        }

        int mid = (start + ending) / 2;

        update(start, mid, 2 * node + 1, l, r, value);

        update(mid + 1, ending, 2 * node + 2, l, r, value);

        st[node] = min(st[node * 2 + 1], st[node * 2 + 2]);

        return;
    }

    int query(int l, int r)
    {
        return query(0, n - 1, l, r, 0);
    }

    void update(int l, int r, int x)
    {
        update(0, n - 1, 0, l, r, x);
    }
};

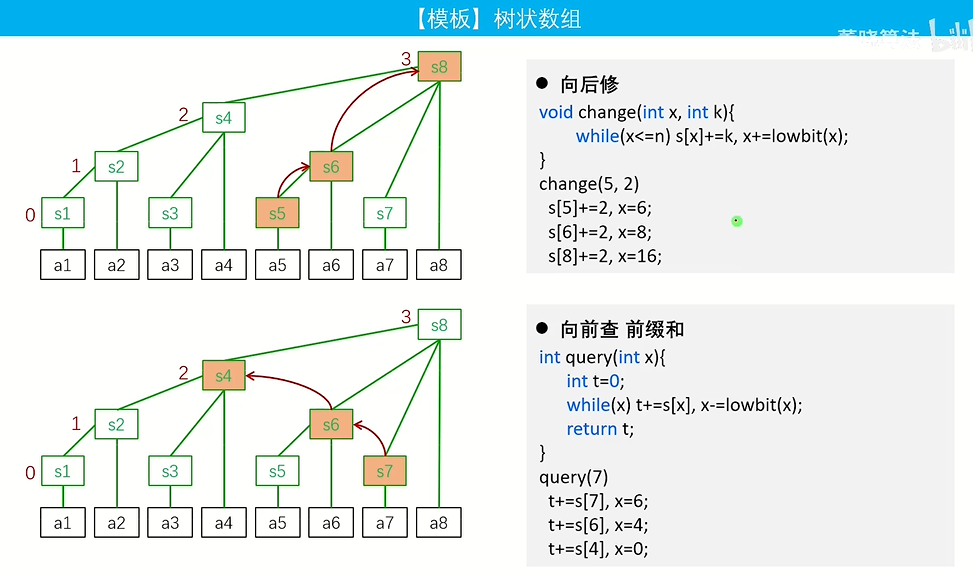
树状数组

(Binary Indexed Tree)

利用数的二进制特征进行检索的树状结构

主要用于对一个数组进行区间求和+点修或者区间修改+点查

//董晓算法的板子
int tree[N];

int lowbit(int x){return x&-x;}

void change(int x,int k)//向后修
{//这里的N开大了，实际上是n
    while(x<=N) tree[x]+=k,x+=lowbit(x);
}

int query(int x)//向前查
{
    int t=0;
    while(x) t+=tree[x],x-=lowbit(x);
    return t;
}

int query(int l,int r)//区间和==前缀和之差
{
    return query(r)-query(l-1);
}

//ACWing板子
int tr[M]
int lowbit(int x)
{
    return x&-x;
}

int query(int x)
{
    int res = 0;
    for(int i=x;i;i-=lowbit(i))
        res+=tr[i];
    return res;
}

void add(int x,int v)
{
    for(int i=x;i<M;i+=lowbit(i))
        tr[i]+=v;
}

封装后直接使用

点修区查

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'

struct FenwickTree {
    vector<int> tree;
    int n;

    FenwickTree() {}
    FenwickTree(int n) {
        init(n);
    }

    void init(int n) {
        this->n = n;
        tree.resize(n + 1, 0);
    }

    int lowbit(int x) {
        return x & -x;
    }

    void update(int x, int k) {
        while (x <= n) {
            tree[x] += k;
            x += lowbit(x);
        }
    }

    int query(int x) {
        int res = 0;
        while (x > 0) {
            res += tree[x];
            x -= lowbit(x);
        }
        return res;
    }

    int query(int l, int r) {
        return query(r) - query(l - 1);
    }
};

void solve() {
    int n, q;
    cin >> n >> q;
    FenwickTree ft(n);

    for (int i = 1; i <= n; i++) {
        int val;
        cin >> val;
        ft.update(i, val);
    }

    while (q--) {
        int a, b, c;
        cin >> a >> b >> c;
        if (a == 0) {
            ft.update(b + 1, c);
        } else {
            cout << ft.query(b + 1, c) << endl;
        }
    }
}

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

区修点查

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'

struct FenwickTree {
    vector<int> tree;
    int n;

    FenwickTree() {}
    FenwickTree(int n) {
        init(n);
    }

    void init(int n) {
        this->n = n;
        tree.resize(n + 1, 0);
    }

    int lowbit(int x) {
        return x & -x;
    }

    void update(int x, int k) {
        while (x <= n) {
            tree[x] += k;
            x += lowbit(x);
        }
    }

    int query(int x) {
        int res = 0;
        while (x > 0) {
            res += tree[x];
            x -= lowbit(x);
        }
        return res;
    }

    int query(int l, int r) {
        return query(r) - query(l - 1);
    }
};

void solve() {
    int n, q;
    cin >> n >> q;
    vector<int> a(n+1);
    FenwickTree ft(n);

    for (int i = 1; i <= n; i++) cin>>a[i];

    while (q--) {
        int op;
        cin >> op;
        if(op==1){
            int l,r,x;
            cin>>l>>r>>x;
            ft.update(l,x);
            ft.update(r+1,-x);
        }else{
            int x;
            cin>>x;
            cout<<a[x]+ft.query(x)<<endl;
        }
    }
}

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

ST表

ST 表（Sparse Table，稀疏表）是用于解决 可重复贡献问题 的数据结构。

ST 表能较好的维护「可重复贡献」的区间信息（同时也应满足结合律），时间复杂度较低，代码量相对其他算法很小。但是，ST 表能维护的信息非常有限，不能较好地扩展，并且不支持修改操作。

// ST表

template<typename T> vector<vector<T>> get_st(vector<T> &v, T (*sel)(T a, T b)) {
    int n = v.size(), m = log2(n)+1;
    vector<vector<T>> ret(m);
    ret[0] = v;
    for(int i=1;i<m;i++) for(int j=0;j<=n-(1<<i);j++) ret[i].push_back(sel(ret[i-1][j],ret[i-1][j+(1<<(i-1))]));
    return ret;
}

template<typename T> T st_queue(vector<vector<T>> &st, int l, int r, T (*sel)(T a, T b)) {
    int lay = log2(r-l+1), wid=1<<lay;
    return sel(st[lay][l],st[lay][r-wid+1]);
}

int get_max(int a, int b) {
    return max(a,b);
}

搜索

递归与回溯

递归

回溯

回溯是递归的副产品，只要有递归就会有回溯。

回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

回溯法，一般可以解决如下几种问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 棋盘问题：N皇后，解数独等等

回溯法解决的问题都可以抽象为树形结构，回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

如图：

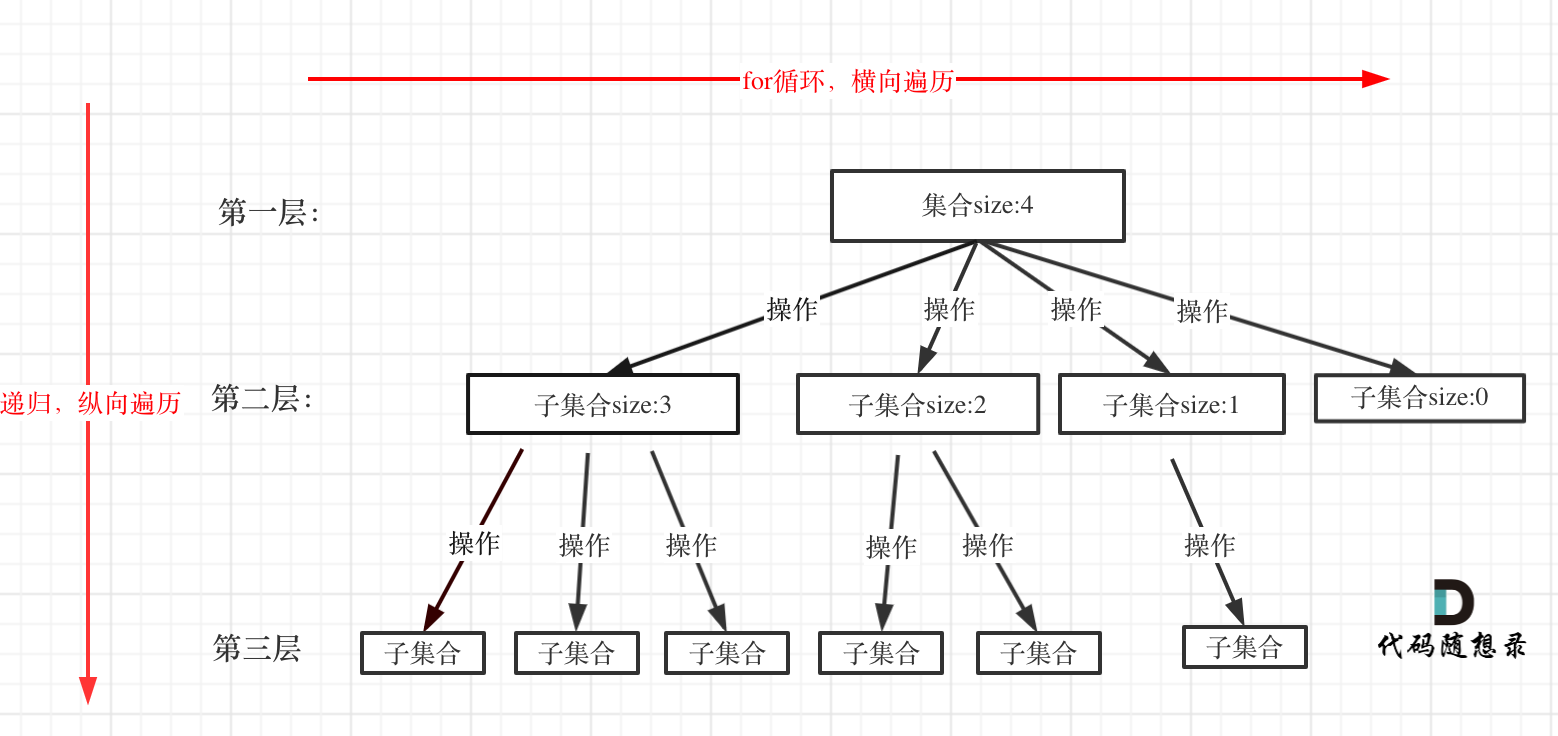
注意图中，我特意举例集合大小和孩子的数量是相等的！

回溯函数遍历过程伪代码如下：

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次。

backtracking这里自己调用自己，实现递归。

大家可以从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

分析完过程，回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

数论

数论的题很多时候是需要数学定理，结论以及证明。

质数与约数

试除法判定质数

bool is_prime(int x)
{
    if(x<2) return false;
    for(int i=2;i<=x/i;i++)
    {
        if(x%i==0) return false;
    }
    return true;
}

试除法分解质因数

void divide(int x)
{
    for(int i=1;i<=x/i;i++)
    {
        if(x%i==0)
        {
            int s=0;
            while(x%i==0) x/=i,s++;
            cout<<i<<" "<<s<<endl;
        }
    }
    if(x>1) cout<<x<<" "<<1<<endl;
    cout<<endl;
}

质因数计数

int N = 1000001;
vector<int> v(N);
for (int i = 2; i < N; i++) {
    if (v[i] == 0) { 
        for (int j = i; j < N; j += i) {
            v[j]++;
        }
    }
}

朴素筛法求素数

int primes[N],cnt;//primes[]存储所有素数
bool vis[N];//vis[x]存储x是否被筛掉

void get_primes(int x)
{
    for(int i=2;i<=n;i++)
    {
        if(vis[i]) continue;
        primes[cnt++]=i;
        for(int j=i;j<=n;j+=i) vis[j]=true;
    }
}

线性筛法求素数

int primes[N],cnt;//primes[]存储所有素数
bool vis[N];//vis[x]存储x是否被筛掉

void get_primes(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]) primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++)
        {
            vis[primes[j]*i]=true;
            if(i%primes[j]==0) break;
        }
    }
}

筛法统计质因数值

const int MX = 1e5;
bool isPrime[MX + 5]; //isPrime[i]代表i这个数是否是质数 false为质数 true不是质数
unordered_map<int, vector<int>> mp; //mp[i]表示i这个数的因数的集合
 
//埃及筛求每个数的因数
//int init = []() {... }(); 立即执行的匿名函数
int init = [](){
    for (int i = 2; i <= MX; i++) {
        if (isPrime[i] == false) {
            //是质数，筛去它的倍数
            for (int j = i; j <= MX; j += i) {
                isPrime[j] = true;
                mp[j].push_back(i);
            }
        }
    }
    return 0;
}();

预处理求质因数指数

const int MAX_N = 10'000;
vector<int> EXP[MAX_N + 1]; 

int init = []() {
    // EXP[x] 为 x 分解质因数后，每个质因数的指数
    for (int x = 2; x <= MAX_N; x++) {
        int t = x;
        for (int i = 2; i * i <= t; i++) {
            int e = 0;
            while(t % i == 0){
                e++;
                t /= i;
            }
            if (e) {
                EXP[x].push_back(e);
            }
        }
        if (t > 1) {
            EXP[x].push_back(1);
        }
    }
    return 0;
}();

试除法求所有约数

vector<int> get_divisors(int x)
{
    vector<int> res;
    for(int i=1;i<=x/i;i++)
    {
        if(x%i==0)
        {
            res.push_back(i);
            if(i!=x/i) res.push_back(x/i);
        }
    }
    sort(res.begin(),res.end());
    return res;
}

约数个数和约数之和

如果有N=${p_1}^{c_1}{p_2}^{c_2}…*{p_k}^{c_k}$

约数个数：$(c_1+1)(c_2+1)…*(c_k+1)$

约数之和：$({p_1}^0+{p_1}^1+…+{p_1}^{c_1})*…({p_k}^0+{p_k}^1+…+{p_k}^{c_k})$

欧几里得算法

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}

扩展欧几里得算法

//求x,y，使得ax+by=gcd(a,b)
int exgcd(int a,int b,int &x,int &y)
{
    if(!b)
    {
        x=1;y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y-=(a/b)*x;
    return d;
}

欧拉函数

描述的是小于或等于n的正整数当中与n互质数的个数

phi(5):就是1、2、3、4、5与5互质数的个数，1、2、3、4，即其值为4

朴素求欧拉函数

int phi(int x)
{
    int res=x;
    for(int i=2;i<=x/i;i++)
    {
        if(x%i==0)
        {
            res=res/i*(i-1);
            while(x%i==0) x/=i;
        }
    }
    if(x>1) res=res/x*(x-1);
    return res;
}

筛法求欧拉函数

int primes[N],cnt;//primes存储所有素数
int euler[N];//存储每一个数的欧拉函数
bool vis[N];//vis[x]存储x是否被筛掉

void get_eulers(int n)
{
    euler[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i])
        {
            primes[cnt++]=i;
            euler[i]=i-1;
        }
    }
    for(int j=0;primes[j]<=n/i;j++)
    {
        int t=primes[j]*i;
        vis[t]=true;
        if(i%primes[j]==0)
        {
            euler[t]=euler[i]*primes[j];
            break;
        }
        euler[t]=euler[i]*(primes[j]-1);
    }
}

费马小定理

中国剩余定理

容斥原理

卷积

快速傅里叶变换

高斯消元

// a[N][N]是增广矩阵
int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )   // 找到绝对值最大的行
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;

        for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);      // 将绝对值最大的行换到最顶端
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];      // 将当前上的首位变成1
        for (int i = r + 1; i < n; i ++ )       // 用当前行将下面所有的列消成0
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2; // 无解
        return 1; // 有无穷多组解
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[i][j] * a[j][n];

    return 0; // 有唯一解
}

组合计数

相关结论

放球问题

• 把 k=3 个无区别的小球放到 n 个有区别的盒子中，允许盒子为空，一个盒子也可以放多个小球，有多少种不同的放法？

递归法求组合数

// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
    for (int j = 0; j <= i; j ++ )
        if (!j) c[i][j] = 1;
        else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

通过预处理逆元的方式求组合数

首先预处理出所有阶乘取模的余数fact[N]，以及所有阶乘取模的逆元infact[N]
如果取模的数是质数，可以用费马小定理求逆元

int qmi(int a, int k, int p)    // 快速幂模板
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
    fact[i] = (LL)fact[i - 1] * i % mod;
    infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}

预处理阶乘及其逆元，每个数的最小质因子，进而快速进行质因数分解，进行组合数计算。

const int MOD = 1'000'000'007;
const int MX = 10013;
const int MX_K = 10001;

long long F[MX]; // F[i] = i!
long long INV_F[MX]; // INV_F[i] = i!^-1
int LPF[MX_K]; // i 的最小质因子是 LPF[i]

long long pow(long long x, int n) {
    long long res = 1;
    for (; n; n /= 2) {
        if (n % 2) {
            res = res * x % MOD;
        }
        x = x * x % MOD;
    }
    return res;
}

auto init = [] {
    F[0] = 1;
    for (int i = 1; i < MX; i++) {
        F[i] = F[i - 1] * i % MOD;
    }

    INV_F[MX - 1] = pow(F[MX - 1], MOD - 2);
    for (int i = MX - 1; i; i--) {
        INV_F[i - 1] = INV_F[i] * i % MOD;
    }

    for (int i = 2; i < MX_K; i++) {
        if (LPF[i] == 0) { // i 是质数
            for (int j = i; j < MX_K; j += i) {
                if (LPF[j] == 0) {
                    LPF[j] = i; // j 的最小质因子是 i
                }
            }
        }
    }
    return 0;
}();

int comb(int n, int m) {
    return F[n] * INV_F[m] % MOD * INV_F[n - m] % MOD;
}

Lucas定理

若p是质数，则对于任意整数 $1 <= m <= n$，有：
$C_n^m = C_{n%p}^{m%p} * C_{n / p}^{m / p} (%p)$

int qmi(int a, int k)       // 快速幂模板
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int C(int a, int b)     // 通过定理求组合数C(a, b)
{
    int res = 1;
    for (int i = 1, j = a; i <= b; i ++, j -- )
    {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i, p - 2) % p;
    }
    return res;
}


int lucas(LL a, LL b)
{
    if (a < p && b < p) return C(a, b);
    return (LL)C(a % p, b % p) * lucas(a / p, b / p) % p;
}

分解质因数法求组合数

当我们需要求出组合数的真实值，而非对某个数的余数时，分解质因数的方式比较好用：

1. 筛法求出范围内的所有质数
2. 通过 $$ C_a^b = \frac{a!(a - b)!}{b!} $$ 这个公式求出每个质因子的次数。 $n! $中$p$的次数是$$ \frac{n}{p} + \frac{n}{p^2}+ \frac{n}{p^3} + … $$
3. 用高精度乘法将所有质因子相乘

int primes[N], cnt;     // 存储所有质数
int sum[N];     // 存储每个质数的次数
bool st[N];     // 存储每个数是否已被筛掉


void get_primes(int n)      // 线性筛法求素数
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)       // 求n！中的次数
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)       // 高精度乘低精度模板
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }

    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    
    return c;

}

get_primes(a);  // 预处理范围内的所有质数

for (int i = 0; i < cnt; i ++ )     // 求每个质因数的次数
{
    int p = primes[i];
    sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}

vector<int> res;
res.push_back(1);

for (int i = 0; i < cnt; i ++ )     // 用高精度乘法将所有质因子相乘
    for (int j = 0; j < sum[i]; j ++ )
        res = mul(res, primes[i]);

卡特兰数

给定n个0和n个1，它们按照某种顺序排成长度为2n的序列，满足任意前缀中0的个数都不少于1的个数的序列的数量为：$$ Cat(n) = \frac{C_{2n}^n}{(n + 1)}$$

简单博弈论

NIM游戏

给定N堆物品，第i堆物品有$A_i$个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。

我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。
所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。
NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

定理： NIM博弈先手必胜，当且仅当 $A_1$ ^$A_2$ ^ … ^ $A_n$ != 0

公平组合游戏ICG

若一个游戏满足：

1.由两名玩家交替行动；
2.在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关；
3.不能行动的玩家判负；
则称该游戏为一个公平组合游戏。
NIM博弈属于公平组合游戏，但城建的棋类游戏，比如围棋，就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子，胜负判定也比较复杂，不满足条件2和条件3。

有向图游戏

给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把每个局面看成图中的一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。

Mex运算

设S表示一个非负整数集合。定义$mex(S)$为求出不属于集合S的最小非负整数的运算，即：
$mex(S) = min(x)$, x属于自然数，且x不属于S

SG函数

在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达节点$y_1, y_2, …, y_k$，定义$$SG(x)$$为x的后继节点$y_1, y_2, …, y_k$ 的SG函数值构成的集合再执行$$mex(S)$$运算的结果，即：
$SG(x) = mex({SG(y_1), SG(y_2), …, SG(y_k)})$
特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即$SG(G) = SG(s)$。

有向图游戏的和

设$$G_1, G_2, …, G_m $$是m个有向图游戏。定义有向图游戏G，它的行动规则是任选某个有向图游戏$G_i$，并在$G_i$上行动一步。G被称为有向图游戏$$G_1, G_2, …, G_m$$的和。
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和，即：
$SG(G) = SG(G_1)$ ^ $SG(G_2) $^ … ^ $SG(G_m)$

定理
有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。
有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。

图论

图论的题核心在与如何将题目的图建出来。

树与图的存储

树是一种特殊的图，与图的存储方式相同

无向图是可以看成存了两个方向的有向图

对于无向图中的边ab,存储两条有向边a->b,b->a

稠密图用邻接矩阵，稀疏图用邻接表

邻接矩阵

g[a][b]; //存储边a->b
    
vector<int> e[N];

邻接表

//对于每个点k,开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头节点
int h[N],e[N],ne[N],idx;

//添加一条边a->b
void insert(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

//初始化
idx=0;
memset(h,-1,sizeof h);

树与图的遍历

时间复杂度O(n+m),n表示点数，m表示边数

深度优先搜索(DFS)

一条路走到底

void dfs(int u)
{
    vis[u]=true;//vis[u]表示点u已经被遍历过
    //点u就是被搜到的点
    for(int i=h[u];i!=-1;i=ne[i])
    {//遍历邻接表
        int j=e[i];
        if(!vis[j]) dfs(j);//没搜过的结点就继续dfs
    }
}

迷宫问题

走迷宫

跳马问题

八皇后问题

思路1

思路2

宽度优先搜索(BFS)

每个分叉先走旁边，每次搜索的位置都是距离当前节点最近的点。因此，BFS是具有最短路的性质的。队列保证本层搜完才进入下一层。

手写队列

void bfs(){
    queue<int> q;
    vis[1]=true;//表示1号点已经被遍历过
    q.push(1);//标记该点被搜，并入队

    while(q.size())
    {//队列不空就一直循环
        int t=q.front();//队头就是搜的点
        q.pop();//取出顶点，处理下一个点

        for(int i=h[t];i!=-1;i=ne[i])
        {//遍历邻接表
            int j=e[i];
            if(!vis[j])
            {//没搜过的结点就入队
                vis[j]=true;//表示点j已经被遍历过
                q.push(j);
            }
        }
    }
}

使用stl的queue容器

题目：走迷宫

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N=110;
typedef pair<int,int> PII;
int map[N][N],mark[N][N];//map存图，mark标记是否搜过，这里兼顾了走了多远
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1},n,m,ans;
void bfs()
{
    memset(mark,-1,sizeof mark);//初始化，表示没来过
    queue<PII>q;
    q.push({0,0});//起点入队
    mark[0][0]=0;
    while(!q.empty())
    {
        PII top=q.front();//以队列中的每个元素为起点
        for(int i=0;i<4;i++)//向四个方向搜索
        {
            int nex=top.first+dx[i],ney=top.second+dy[i];//下一个点
            if(nex>=0&&nex<n&&ney>=0&&ney<m&&mark[nex][ney]==-1&&map[nex][ney]==0)
            {//位置合法且未搜索过
                mark[nex][ney]=mark[top.first][top.second]+1;//标记
                q.push({nex,ney});//入队，之后要在该节点为起点搜那一层
            }
        }
        q.pop();//当前结点的所有搜索结束，这个点就出队
    }
    cout<<mark[n-1][m-1];//最先走到的就是最短路，因为mark标记了走过的路不会再走，所以每个点记录的路程都是最短路
}
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            scanf("%d",&map[i][j]);
        }
    }
    bfs();
}

0-1BFS

一种变体，专门用于边权仅包含 0 和 1 的图。

0-1 BFS 的核心在于使用双端队列（deque）来优化搜索过程：

• 边权为 0 的边： 当从当前节点通过一条权重为 0 的边到达下一个节点时，由于这条边不会增加路径长度，因此将该节点插入队列的前端（push_front）。
• 边权为 1 的边： 当通过一条权重为 1 的边到达下一个节点时，路径长度增加 1，因此将该节点插入队列的末端（push_back）。

const int INF = 0x3f3f3f3f;
const int dx[4] = {-1, 1, 0, 0}; 
const int dy[4] = {0, 0, -1, 1};

void solve() {
    int H, W, A, B, C, D;
    cin >> H >> W;
    vector<string> grid(H);
    for (int i = 0; i < H; i++) cin >> grid[i];
    cin >> A >> B >> C >> D;
    --A; --B; --C; --D; 

    vector<vector<int>> dist(H, vector<int>(W, INF));
    deque<pair<int,int>> dq;
    dist[A][B] = 0;
    dq.push_front({A, B});

    while (!dq.empty()) {
        auto [x, y] = dq.front();
        dq.pop_front();

        for (int d = 0; d < 4; d++) {
            int nx = x + dx[d], ny = y + dy[d];
            if (nx >= 0 && nx < H && ny >= 0 && ny < W && grid[nx][ny] == '.' && dist[nx][ny] > dist[x][y]) {
                dist[nx][ny] = dist[x][y];
                dq.push_front({nx, ny});
            }
        }

        for (int d = 0; d < 4; d++) {
            for (int step = 1; step <= 2; step++) {
                int nx = x + dx[d] * step, ny = y + dy[d] * step;
                if (nx >= 0 && nx < H && ny >= 0 && ny < W && dist[nx][ny] > dist[x][y] + 1) {
                    dist[nx][ny] = dist[x][y] + 1;
                    dq.push_back({nx, ny});
                }
            }
        }
    }
    cout<< dist[C][D] << endl;
}

拓扑排序

首先要确定图是有向无环图才有拓扑序

时间复杂度O(n+m)

bool topsort()
{
    int hh=0,tt=-1;
    
    //d[i]存储点的入度
    for(int i=1;i<=n;i++)
    {
        if(!d[i]) q[++tt]=i;
    }
    
    while(hh<=tt)
    {
        int t=q[hh++];
        
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=ne[i];
            if(--d[j]==0) q[++tt]=j;
        }
    }
    
    //如果所有点都入队了，说明存在拓扑序，否则不存在
    return tt=n-1;
}

朴素拓扑排序

#include<iostream>
#include<cstring>
using namespace std;
//拓扑排序模板
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx = 0;
int q[N], d[N];

void add(int a,int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void init()
{
    idx = 0;
    memset(h, -1, sizeof h);
}

void topsort()
{
    int hh=0,tt=-1;

    for (int i = 1; i <= n; i++)
    {//看题目的结点是从0开始还是从1开始
        //cout<<d[i]<<" ";
        if (!d[i])
        {
            q[++tt] = i;
            //cout<<i<<" ";
        }
        
    }

    while (hh<=tt)
    {
        int t = q[hh++];
        //cout<<t<<" ";

        for (int i = h[t]; i != -1; i=ne[i])
        {
            int j = e[i];
            if (--d[j]==0)
            {
                q[++tt] = j;
            }
            
        }
        
    }
    // return tt=n-1;
    //如果需要判断有无拓扑序
}
int main()
{
    init();
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
        d[b]++;
    }
    /*
    for (auto i:d)
    {
        cout<<i<<" ";
    }
    */
    topsort();
    for (int i = 0; i < n; i++) 
    {
        cout << q[i] << " ";
    }
    return 0;
}

字典序拓扑排序

#include <iostream>
#include <cstring>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
//字典序拓扑排序
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx = 0;
int d[N];
vector<int> ans;
priority_queue<int, vector<int>, greater<int>> pq;  // 优先队列，按照从小到大的顺序出队

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void init()
{
    idx = 0;
    memset(h, -1, sizeof h);
}

void topsort()
{
    for (int i = 0; i < n; i++)
    {
        if (!d[i])
        {
            pq.push(i);
        }
    }

    while (!pq.empty())
    {
        int t = pq.top();
        pq.pop();
        //t就是拓扑序列的数
        cout << t << " ";
        // ans.push_back(t);
        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (--d[j] == 0)
            {
                pq.push(j);
            }
        }
    }
    // return ans.size()==n;
}

int main()
{
    init();
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
        d[b]++;
    }

    topsort();

    return 0;
}

最短路

朴素dijkstra算法

基于贪心

int g[N][N];//存储每条边
int dist[N];//存储1号点到每个点的最短距离
bool vis[N];//存储每个点的最短路是否已经确定

//求1号点到n号点的最短路，不存在则返回-1
int dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    
    for(int i=0;i<n-1;i++)
    {
        int t=-1;//在还未确定最短路的点中寻找距离最小的点
        for(int j=1;j<=n;j++)
        {
            if(!vis[j]&&t==-1||dist[t]>dist[j]) t=j;
        }
        
        //用t更新其他点的距离
        for(int j=1;j<=n;j++)
        {
            dist[j]=min(dist[j],dist[t]+g[t][j]);
        }
        
        vis[t]=true;
    }
    
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}

堆优化版dijkstra算法

typedef pair<int,int> PII;

int n;//点的数量
int h[N],w[N],e[N],ne[N],idx;//邻接表存所有边
int dist[N];//存储所有点到1号点的距离
bool vis[N];//存储每个点的最短距离是否已确定

//求1号点到n号点的最短距离，如果不存在，返回-1
int dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    priority_queue<PII,vector<PII>,greater<PII>> heap;
    heap.push({0,1});//first存储距离，second存储节点编号
    
    while(heap.size())
    {
        auto t=heap.top();
        heap.pop();
        
        int ver=t.second,distance=t.first;
        
        if(!vis[ver]) continue;
        vis[ver]=true;
        
        for(int i=h[ver];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>distance+w[i])
            {
                dist[i]=distance+w[i];
                heap.push({dist[j],j});
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}

Bellman-Ford算法

基于动态规划

int n,m;//n表示点数，m表示边数
int dist[N];//dist[x]存储1到x的最短路距离

struct Edge//边，a表示出点，b表示入点，w表示边的权重
{
    int a,b,w;
}edges[M];

//求1到n的最短路距离，如果无法走到，则返回-1
int bellman_ford()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    
    //如果第n次迭代任然会松弛三角不等式，就说明存在一条长度是n+1的最短路径。
    //由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            int a=edges[j].a,b=edges[j].b,w=edges[j].w;
            if(dist[b]>dist[a]+w)
            {
                dist[b]=dist[a]+w;
            }
        }
    }
    
    if(dist[n]>0x3f3f3f3f/2) return -1;
    return dist[n];
}

spfa算法(队列优化的Bellman-Ford)

int n;//总点数
int h[N],w[N],e[N],ne[N],idx;//邻接表存储所有边
int dist[N];//存储每个点到1号点的最短距离
bool vis[N];//存储每个点是否在队列中

//求1号点到n号点的最短路距离，如果从1号点无法走到n号点，返回-1
int spfa()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    
    queue<int> q;
    q.push(1);
    vis[1]=true;
    
    while(q.size())
    {
        auto t=q.front();
        q.pop();
        
        vis[t]=false;
        
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[t]+w[i])
            {
                dist[j]=dist[t]+w[i];
                if(!vis[j])//如果队列中已存在j,则不需要重复将j插入
                {
                    q.push(j);
                    vis[j]=true;
                }
            }
        }
    }
    
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}

spfa判断图中是否存在负环

int n;//总点数
int h[N],w[N],e[N],ne[N],idx;//邻接表存所有边
int dist[N],cnt[N];//dist[]存储1到x的最短路距离，cnt[]存储1到x的最短路中经过的点数
bool vis[N];//存储每个点是否在队列中

//如果存在负环，返回true，否则返回false
bool spfa()
{
    //不需要初始化dist数组
    //原理：如果某条最短路上有n个点(除了自己)，那么加上自己一共有n+1点，由抽屉原理，一定有两个点相同，所有存在环。
    
    queue<int> q;
    for(int i=1;i<=n;i++)
    {
        q.push(i);
        vis[i]=true;
    }
    
    while(q.size())
    {
        auto t=q.front();
        q.pop();
        
        vis[t]=false;
        
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[t]+w[i])
            {
                dist[j]=dist[t]+w[i];
                cnt[j]=cnt[t]+1;
                if(cnt[j]>=n) return true;//如果从1到x的最短路中包含至少n个点(不包括自己)，则说明存在环
                if(!vis[j])
                {
                    q.push(j);
                    vis[j]=true;
                }
            }
        }
    }
    
    return false;
}

Floyd算法

//初始化
for(int i=1;i<=n;i++)
{
    for(int j=1;j<=n;j++)
    {
        if(i==j) d[i][j]=0;
        else d[i][j]=INF;//INF是一个极大的数
    }
}

//算法结束后，d[a][b]表示a到b的最短距离
void floyd()
{
    for(int k=1;k<=n;k++)
    {
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
            }
        }
    }
}

最小生成树

Prim算法

int n;//n表示点数
int g[N][N];//邻接矩阵，存储所有边
int dist[N];//存储其他点到当前最小生成树的距离
bool vis[N];//存储每个点是否已经在生成树中

//如果图不联通，返回INF(0x3f3f3f3f),否则返回最小生成树的树边权重之和
int prim()
{
    memset(dist,0x3f,sizeof dist);
    
    int res=0;
    for(int i=0;i<n;i++)
    {
        int t=-1;
        for(int j=1;j<=n;j++)
        {
            if(!vis[j]&&(t==-1||dist[t]>dist[j])) t=j;
        }
        if(i&&dist[t]==INF) return INF;
        
        if(i) res+=dist[t];
        vis[t]=true;
        
        for(int j=1;j<=n;j++) dist[j]=min(dist[j],g[t][j]);
    }
    
    return res;
}

Kruskal算法

int n,m;//n是点数，m是边数
int p[N];//并查集父节点数组

struct Edge//存储边
{
    int a,b,w;
    
    bool operator<(const Edge &W)const{
        return w<W.w;
    }
}edges[M];

int find(int x)//并查集核心操作
{
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges,edges+m);
    
    for(int i=1;i<=n;i++) p[i]=i;//并查集初始化
    
    int res=0,cnt=0;
    for(int i=0;i<m;i++)
    {
        int a=edges[i].a,b=edges[i].b,w=edges[i].w;
        
        a=find(a),b=find(b);
        if(a!=b)//如果两个连通块不连通，就合并
        {
            p[a]=b;
            res+=w;
            cnt++;
        }
    }
    
    if(cnt<n-1) return INF;
    return res;
}

二分图

染色法判别二分图

int n;//n表示点数
int h[N],e[N],ne[N],idx;//邻接表存储图
int color[N];//表示每个点的颜色，-1表示未染色，0表示白色，1表示黑色

//u表示当前节点，c表示当前点的颜色
bool dfs(int u,int c)
{
    color[u]=c;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(color[j]==-1)
        {
            if(!dfs(j,!c)) return false;
        }
        else if(color[j]==c) return false;
    }
    
    return true;
}

bool check()
{
    memset(color,-1,sizeof color);
    bool flag=true;
    for(int i=1;i<=n;i++)
    {
        if(!dfs(i,0))
        {
            flag=false;
            break;
        }
    }
    return flag;
}

匈牙利算法

int n1,n2;//n1表示第一个集合中的点数，n2表示第二个集合中的点数
int h[N],e[N],ne[N],idx;//邻接表 存储所有边，匈牙利算法只会用到第二个集合指向第一个集合的边，所以只用存一个方向的边
int match[N];//存储第二个集合中每个点当前匹配的第一个集合中的点是哪个
bool vis[N];//表示第二个集合中每个点是否已经被遍历过

bool find(int x)
{
    for(int i=h[x];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(!vis[j])
        {
            vis[j]=true;
            if(match[j]==0||find(match[j]))
            {
                match[j]=x;
                return true;
            }
        }
    }
    
    return false;
}

//求最大匹配数，依次枚举第一个集合中的每一个点能否匹配第二个集合中的点
int res=0;
for(int i=1;i<=n1;i++)
{
    memset(vis,false,sizeod vis);
    if(find(i)) res++;
}

强连通分量

最近公共祖先(LCA)

倍增算法

const int N=5e5+10;
int n,m,s;//n表示树的结点个数，m表示询问个数，s表示树根节点的序号
vector<int> e[N];//使用邻接矩阵存，这个需要scanf()+printf()才可以过洛谷3379
int dep[N],fa[N][20];
void dfs(int u,int father){
    dep[u]=dep[father]+1;
    //向上跳1、2、4...步的祖先
    fa[u][0]=father;
    for(int i=1;i<=19;i++){
        fa[u][i]=fa[fa[u][i-1]][i-1];
    }
    for(int v:e[u]){
        if(v!=father) dfs(v,u);
    }
}

int lca(int u,int v){
    if(dep[u]<dep[v]) swap(u,v);
    //先跳到同一层
    for(int i=19;i>=0;i--){
        if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
    }
    if(u==v) return v;
    //再跳到LCA的下一层
    for(int i=19;i>=0;i--){
        if(fa[u][i]!=fa[v][i]){
            u=fa[u][i];
            v=fa[v][i];
        }
    }
    return fa[u][0];
}
int main(){
  scanf("%d%d%d", &n,&m,&s);
  for(int i=1; i<n; i++){
    scanf("%d%d",&a,&b);
    add(a,b); 
    add(b,a);
  }
  dfs(s, 0);
  while(m--){
    scanf("%d%d", &a, &b);
    printf("%d\n",lca(a, b));
  }
  return 0;
}

//优化方案
const int N=5e5+10,M=2*N; 
int n,m,s,a,b;
int dep[N],fa[N][22];
int h[N],to[M],ne[M],tot;//使用邻接表存
void add(int a, int b){
  to[++tot]=b,ne[tot]=h[a],h[a]=tot;
}
void dfs(int x, int f){
  dep[x]=dep[f]+1; 
  fa[x][0]=f;
  for(int i=0; i<=20; i++){//遍历邻接表
      fa[x][i+1]=fa[fa[x][i]][i];
  } 
     
  for(int i=h[x]; i; i=ne[i]){
      if(to[i]!=f) dfs(to[i], x);
  }
}
int lca(int x, int y){
  if(dep[x]<dep[y]) swap(x, y);
  for(int i=20; ~i; i--){
      if(dep[fa[x][i]]>=dep[y]) x=fa[x][i];
  }
  if(x==y) return y;
  for(int i=20; ~i; i--){
      if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
  }  
  return fa[x][0];
}
int main(){
  cin>>n>>m>>s;
  for(int i=1; i<n; i++){
    cin>>a>>b;
    add(a,b); 
    add(b,a);
  }
  dfs(s, 0);
  while(m--){
    cin>>a>>b;
    cout<<lca(a,b)<<endl;
  }
  return 0;
}

Tarjan算法

const int N=5e5+10;
M=2*N;
int n,m,s;
vector<int> e[N];
vector<pair<int,int>> query[N];
int fa[N],vis[N],ans[M];
int find(int x){
    if(fa[x]!=x) fa[x]=find(fa[x]);
    return fa[x];
}
void tarjan(int u)
{
    vis[u]=true;//入u时，标记u
    for(auto v:e[u]){
        if(!vis[v]){
            tarjan(v);
            fa[v]=u;//回u时，v指向u
        }
    }
    //离u时，枚举LCA
    for(auto q:query[u]){
        int v=q.first,i=q.second;
        if(vis[v]) ans[i]=find(v);
    }
}
int main()
{
    cin>>n>>m>>s;
    int a,b;
    for(int i=1; i<n; i++){
      cin>>a>>b;//存图
      e[a].push_back(b);
      e[b].push_back(a);
    }
    for(int i=1;i<=m;i++){
      cin>>a>>b;//存查询
      query[a].push_back({b,i});
      query[b].push_back({a,i});
     }
    for(int i=1;i<=N;i++)fa[i]=i;//并查集初始化
    tarjan(s);
    for(int i=1; i<=m; i++){
        cout<<ans[i]<<endl;
    }
  return 0;
}

树链剖分

vector<int> e[N];
int fa[N],dep[N],son[N],sz[N];
int top[N];
void dfs1(int u,int father){//搞出fa,dep,son
    fa[u]=father,dep[u]=dep[father]+1,sz[u]=1;
    for(int v:e[u]){
        if(v==father) continue;
        dfs1(v,u);
        sz[u]+=sz[v];
        if(sz[son[u]]<sz[v]) son[u]=v;
    }
}
void dfs2(int u,int t){//搞出top
    top[u]=t;//记录链头
    if(!son[u]) return;//无重儿子返回
    dfs2(son[u],t);//搜重儿子
    for(int v:e[u]){
        if(v==fa[u]||v==son[u]) continue;
        dfs2(v,v);//搜轻儿子
    }
}
int lca(int u,int v){
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]]) swap(u,v);
        u=fa[top[u]];
    }
    return dep[u]<dep[v]?u:v;
}
int main()
{
    cin >> n >> m >> s;
    int a, b;
    for (int i = 1; i < n; i++){
        cin >> a >> b;
        e[a].push_back(b);
        e[b].push_back(a);
    }
    dfs1(s, 0);
    dfs2(s, s);
    while (m--){
        cin >> a >> b;
        cout << lca(a, b) << endl;
    }
    return 0;
}

构造

计算几何

算法思想

动态规划

如果某一问题有很多重叠子问题，使用动态规划是最有效的。

动态规划中每一个状态一定是由上一个状态推导出来的。

对于动态规划问题，拆解为如下五步曲

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！

分析框架

记忆化搜索

背包问题

线性DP

数字三角形模型

摘花生

最长上升子序列模型(LIS)

区间DP

计数类DP

数位统计DP

数位 DP 通常利用“位与位之间”的关系来设计状态（例如当前位置、是否已达上界、前导零情况以及其他辅助信息如模状态）（从最高位到最低位一个个确定数字）

题目链接

class Solution {
public:
    int countSpecialNumbers(int n) {
        string s = to_string(n);
        int m = s.length();
        vector<vector<int>> memo(m, vector<int>(1 << 10, -1)); // -1 表示没有计算过
        auto dfs = [&](auto&& dfs, int i, int mask, bool is_limit, bool is_num) -> int {
            if (i == m) {
                return is_num; // is_num 为 true 表示得到了一个合法数字
            }
            if (!is_limit && is_num && memo[i][mask] != -1) {
                return memo[i][mask]; // 之前计算过
            }
            int res = 0;
            if (!is_num) { // 可以跳过当前数位
                res = dfs(dfs, i + 1, mask, false, false);
            }
            // 如果前面填的数字都和 n 的一样，那么这一位至多填数字 s[i]（否则就超过 n 啦）
            int up = is_limit ? s[i] - '0' : 9;
            // 枚举要填入的数字 d
            // 如果前面没有填数字，则必须从 1 开始（因为不能有前导零）
            for (int d = is_num ? 0 : 1; d <= up; d++) {
                if ((mask >> d & 1) == 0) { // d 不在 mask 中，说明之前没有填过 d
                    res += dfs(dfs, i + 1, mask | (1 << d), is_limit && d == up, true);
                }
            }
            if (!is_limit && is_num) {
                memo[i][mask] = res; // 记忆化
            }
            return res;
        };
        return dfs(dfs, 0, 0, true, false);
    }
};

上下界数位dp

题目链接

class Solution {
public:
    long long numberOfPowerfulInt(long long start, long long finish, int limit, string s) {
        string low = to_string(start);
        string high = to_string(finish);
        int n = high.size();
        low = string(n - low.size(), '0') + low; // 补前导零，和 high 对齐
        int diff = n - s.size();

        vector<long long> memo(n, -1);
        auto dfs = [&](this auto&& dfs, int i, bool limit_low, bool limit_high) -> long long {
            if (i == low.size()) {
                return 1;
            }

            if (!limit_low && !limit_high && memo[i] != -1) {
                return memo[i]; // 之前计算过
            }

            // 第 i 个数位可以从 lo 枚举到 hi
            // 如果对数位还有其它约束，应当只在下面的 for 循环做限制，不应修改 lo 或 hi
            int lo = limit_low ? low[i] - '0' : 0;
            int hi = limit_high ? high[i] - '0' : 9;

            long long res = 0;
            if (i < diff) { // 枚举这个数位填什么
                for (int d = lo; d <= min(hi, limit); d++) {
                    res += dfs(i + 1, limit_low && d == lo, limit_high && d == hi);
                }
            } else { // 这个数位只能填 s[i-diff]
                int x = s[i - diff] - '0';
                if (lo <= x && x <= hi) { // 题目保证 x <= limit，无需判断
                    res = dfs(i + 1, limit_low && x == lo, limit_high && x == hi);
                }
            }

            if (!limit_low && !limit_high) {
                memo[i] = res; // 记忆化 (i,false,false)
            }
            return res;
        };
        return dfs(0, true, true);
    }
};

状态压缩DP

树形DP

贪心

单峰的情况下，才有贪心的可能性

总选择局部最优解，以获得全局最优解

贪心算法一般分为如下四步：

• 将问题分解为若干个子问题
• 找出适合的贪心策略
• 求解每一个子问题的最优解
• 将局部最优解堆叠成全局最优解

这个四步其实过于理论化了，平时在做贪心类的题目，很难去按照这四步去思考。

做题的时候，只要想清楚 局部最优 是什么，如果推导出全局最优，其实就够了。

如何验证可不可以用贪心算法呢？

最好用的策略就是举反例，如果想不到反例，那么就试一试贪心吧。

如果认为举例子得出的结论不靠谱，想要严格的数学证明。

一般数学证明有如下两种方法：

• 数学归纳法
• 反证法

枚举

一一枚举结果。

分治

将问题分解，分而治之。

将一个复杂的问题，分成两个或多个相似的子问题，在把子问题分成更小的子问题，直到更小的子问题可以简单求解，求解子问题，则原问题的解则为子问题解的合并。

当出现满足以下条件的问题：

• 原始问题可以分成多个相似的子问题
• 子问题可以很简单的求解
• 原始问题的解是子问题解的合并
• 各个子问题是相互独立的，不包含相同的子问题

分治的解题策略：

• 第一步：分解，将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
• 第二步：解决，解决各个子问题
• 第三步：合并，将各个子问题的解合并为原问题的解

其他

高精度

高精度加法

vector<int> add(vector<int> &A,vector<int> &B)
{//C=A+B,满足A>=0,B>=0
    if(A.size()<B.size()) return add(B,A);
    
    vector<int> C;
    int t=0;
    for(int i=0;i<A.size();i++)
    {
        t+=A[i];
        if(i<B.size()) t+=B[i];
        C.push_back(t%10);
        t/=10;
    }
    
    if(t) C.push_back(t);
    return C;
}

高精度减法

vector<int> div(vector<int> &A,vector<int> &B)
{//C=A-B,满足A>=B,A>=0,B>=0
    vector<int> C;
    for(int i=0,t=0;i<A.size();i++)
    {
        t=A[i]-t;
        if(i<B.size()) t-=B[i];
        C.push_back((t+10)%10);
        if(t<0) t=1;
        else t=0;
    }
    
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}

高精度乘低精度

vector<int> mul(vector<int> &A,int b)
{//C=A*b,满足A>=0,b>0
    vector<int> C;
    int t=0;
    for(int i=0;i<A.size()||t;i++)
    {
        if(i<A.size()) t+=A[i]*b;
        C.push_back(t%10);
        t/=10;
    }
    
    return C;
}

高精度除以低精度

vector<int> div(vector<int> &A,int b,int &r)
{//A/b=C...r,满足A>=0,b>0
    vector<int> C;
    r=0;
    for(int i=A.size()-1;i>=0;i--)
    {
        r=r*10+A[i];
        C.push_back(r/b);
        r%=b;
    }
    reverse(C.begin(),C.end());
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}

高精度乘高精度

vector<int> mul(vector<int> &A,vector<int> &B)
{//C=A*B,满足A>=0,B>=0
    vector<int> C(A.size()+B.size(),0);
    
    int t=0;
    for(int i=0;i<A.size();i++)
    {
        for(int j=0;j<B.size();j++)
        {
            t+=A[i]*B[i]+C[i+j];
            C[i+j]=t%10;
            t/=10;
        }
        int k=B.size();
        if(t)
        {
            C[i+k]=t%10;
            t/=10;
            k++;
        }
    }
    while(C[C.size()-1]==0&&C.size()>1) C.pop_back();
    
    return C;
}

高精度如何输入输出数据？

以字符串输入，逆序存入数组，逆序输出数组

using namespace std;
//以高精度乘高精度举例
int main()
{
    string a,b;
    cin>>a>>b;
    vector<int> A,B;
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
    
    vector<int> C=mul(A,B);
    for(int i=C.size()-1;i>=0;i--) printf("%d",C[i]);
    
    return 0;
}

阶乘之和

//length为所求的阶乘（答案）的位数，n为求1到n的阶乘之和
string Bigfact(int length,int n)
{
    int a[length]={0},sum[length]={0};//a数组放阶乘，sum数组放阶乘之和，这两个数组一定要初始化；
    a[0]=1;//1的阶乘为1
    sum[0]=1;//1的阶乘没有可加了，所以阶乘之和为1
    if(n==1) return "1";
    for(int i=2;i<=n;i++)
    {
        //计算从1到i的阶乘之和
        for(int j=0;j<length;j++){a[j]*=i;}//计算i的阶乘，每一位上都要乘以i，因为没有去除0的操作，所以数位为零的就不用管，依旧是0
        for(int j=0;j<length;j++)
        {//length其实代表的是那一个数最多有多少位；
            if(a[j]>=10)
            {//当一位数大于10或者等于10的时候就不是一位数了，是两位，所以要往前进一
                a[j+1]+=a[j]/10;//进位运算把十位往前进一位
                a[j]%=10;//留下个位
            }
            sum[j]+=a[j];//相当于每一个位对应相加
            if(sum[j]>=10)
            {
              sum[j+1]++;//进位运算：和乘法不一样，两个一位数相加只能进一，例如6+8=12，进1留2，乘法则可以进更多，例如：4*6=24，进2留4
              sum[j]-=10;//加法留个位就可以用减10
            }
        }
    }
    int p=length-1;//数组下标是用长度减一；
    while(sum[p]==0)p--;//删除默认值为0的，意思就是00001111变成1111从右往左是第一位
    string ans="";
    while(p>=0){ans+=sum[p]+'0';p--;}//从最高位开始输出：p--来控制往后输出；意思就是从最高位输出到最后一位，例如：1435，先输出千位1然后百位4十位3依次类推
    return ans;
}

快速幂

常用小技巧，快速求幂

朴素快速幂

//求m^k mod p 时间复杂度O(logk)
ll qmi(int m,int k,int p)
{
    ll res=1%p,t=m;
    while(k)
    {
        if(k&1) res=res*t%p;
        t=t*t%p;
        k>>=1;
    }
    return res;
}

矩阵快速幂

前缀和与差分

前缀和与差分互为逆运算

一维前缀和

s[i]=a[1]+a[2]+…+a[i];
a[l]+…+a[r]=s[r]-s[l-1];

cin>>a[i];
a[i]+=a[i];//不保留原数组

s[i]=s[i-1]+a[i];//保留原数组，开新数组存前缀和

sum[l,r]//求[l,r]的区间和
s[r]-s[l-1]

二维前缀和

s[i,j]=第i行第j列格子左上部分所有元素之和
以(x1,y1)为左上角，（x2,y2）为右下角的子矩阵和
s[x2,y2]-s[x1-1,y2]-s[x2,y1-1]+s[x1-1,y1-1]

cin>>a[i][j];    
a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];//不保留原数组

s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];//保留原数组，开新数组存前缀和

//以(x1,y1)为左上角，（x2,y2）为右下角的子矩阵和
s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]

前缀异或

前缀异或s[i] = s[i - 1] ^ a[i]。

每个 s[i] 的值等于前 i 个数字的异或结果。

由于异或运算的逆运算是它本身，也就是说两次异或同一个数最后结果不变，即(a ^ b) ^ b = a，则每次询问(l,r)区间，输出s[r]^s[l-1]。

for (int i = 1; i <= n;i++){
    cin >> a[i];
    s[i] = s[i - 1] ^ a[i]; // 前缀异或
}

树上前缀和

//s[x]表示起点到x的前缀和
//(x,y)的路径和
//点前缀和
s[x]+s[y]-s[lca]-s[fa[lca]]
//边前缀和
s[x]+s[y]-2*s[lca]

一维差分

//给区间[l,r]中每个数加上c
void insert(int l,int r,int c)
{
    b[l]+=c,b[r+1]-=c;
}

二维差分

//以(x1,y1)为左上角，（x2,y2）为右下角的子矩阵所有元素加上c
void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1,y1]+=c;
    b[x2+1,y1]-=c;
    b[x1,y2+1]-=c;
    b[x2+1,y2+1]+=c;
}

树上差分

//初态树上权为0，对（x,y）路径均做+1操作
//点差分
d[x]++;
d[y]++;
d[lca]--;
d[fa[lca]]--;
//边差分
d[x]++;
d[y]++;
d[lca]-=2;

商分

题目传送门

类似[差分](# 一维差分)，计算 a 的「商分」，即相邻两数的商。

例如：

a=[2,2,4,8,8] 的商分数组为 q=[2,1,2,2,1]。
a=[1,4,4,8,8] 的商分数组为 q=[1,4,1,2,1]。
不同的 a，唯一对应着不同的 q。计算理想数组 a 的个数，可以转化成计算商分数组 q 的个数。

现在假设 a_n−1=8，也就是所有 q_i 的乘积等于 8，有多少个不同的 q？

这个问题等价于放球问题

离散化

将离散的数据映射到一个小区间内

对数据直接mod一个数也相当于将数据映射在这个区间内

1.排序

2.去重

3.查找

vector<int> alls;//存储所有待离散化的值
sort(alls.begin(),alls.end());//排序
alls.erase(unique(alls.begin(),alls.end()),alls.end());//去重
//二分求出对应离散化的值
int find(int x)
{//找到第一个大于等于x的位置
    int l=0,r=alls.size()-1;
    while(l<r)
    {
        int mid=l+r>>1;
        if(alls[mid]>=x) r=mid;
        else l=mid+1;
    }
    return r+1;//映射到1,2,3...n
}

双指针

先暴力模拟，然后看i和j有什么单调关系，再套模板将时间复杂度降低

常见问题分类：

(1)对于一个序列，用两个指针维护一段区间

(2)对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

for(int i=0,j=0;i<n;i++)
{
    while(j<i&&check(i,j)) j++;
    
    //具体问题的逻辑
}

区间合并

//将所有存在交集的区间合并
#define Pll pair<long long,long long>
void merge(vector<Pll> &segs)
{
    vector<Pll> res;
    
    sort(segs.begin(),segs.end());
    
    int st=-2e9,ed=-2e9;
    for(auto seg:segs)
    {
        if(ed<seg.first)
        {
            if(st!=-2e9) res.push_back({st,ed});
            st=seg.first,ed=seg.second;
        }
        else
        {
            ed=max(ed,seg.second);
        }
    }
    
    if(st!=-2e9) res.push_back({st,ed});
    
    segs=res;
}

有关闰年天数的计算与表达

bool is_leap(int year)
{
    return (year % 4 == 0 && year % 100 != 0) || (year % 400 == 0);
}

int return_days(int year, int month)
{
    int days[] = {31, (int)(is_leap(year) ? 29 : 28), 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
    return days[month - 1];
}

补前导零

setw() 函数只对紧接着的输出产生作用。

当后面紧跟着的输出字段长度小于 n 的时候，在该字段前面用空格补齐，当输出字段长度大于 n 时，全部整体输出。

// 开头设置宽度为 4，后面的 runoob 字符长度大于 4，所以不起作用
cout << setw(4) << "runoob" << endl;
// 中间位置设置宽度为 4，后面的 runoob 字符长度大于 4，所以不起作用
cout << "runoob" << setw(4) << "runoob" << endl;
// 开头设置间距为 14，后面 runoob 字符数为6，前面补充 8 个空格 
cout << setw(14) << "runoob" << endl;
// 中间位置设置间距为 14 ，后面 runoob 字符数为6，前面补充 8 个空格 
cout << "runoob" << setw(14) << "runoob" << endl;

setw() 默认填充的内容为空格，可以 setfill() 配合使用设置其他字符填充。

//补前导零实现
cout << setfill('0')  << setw(5) << 1 << endl;

向上取整、四舍五入

//向上取整
//对一个数/n后向上取整
ll Solve(ll X)
{
    ll result = X / n;
    if (X > 0 && X % n != 0) result += 1;
    //cout << result << endl;
    return result;
}

//范围小的话
ll x;
x=(x+n-1)/n;
cout<<x<<endl;

//四舍五入，没有小数
double kk=1.5;
//kk=1.5;
cout<<(int)(kk+0.5)<<"\%"<<endl;

//四舍五入，有小数
double a=1.235; 
double b=1.234;
printf("printf:a=%.2lf\n",a);
printf("printf:b=%.2lf\n",b);
cout<<"cout:a=";
cout<<fixed<<setprecision(2)<<a<<endl;
cout<<"cout:b=";
cout<<fixed<<setprecision(2)<<b<<endl;

判断回文

//判断一个数是否回文
bool isPalindrome(ll n)
{//将整个数取反后看和原来的数是否相同
    ll t = n, num = 0;
    while (t != 0){
        num = num * 10 + t % 10;
        t /= 10;
    }
    if (num==n) return true;
    else return false;
}
//判断字符串是否回文
bool is_palin(const string s)
{//双指针，一头一尾比较，直到中间两个（奇数的话就是同一个）都是相等
    int i = 0, j = strlen(s) - 1;
    while (i <= j)
        if (s[i++] != s[j--]) return false;
    return true;
}

进制转换

注：这里的k进制主要指2 ，8，10，16之间的转换

二进制B,八进制O,十进制D,十六进制H

k进制转十进制：从低位到高位，按权展开

以二进制转十进制为例

十进制转k进制：除k取余，余数为该位权上的数，而商继续除以k，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。

以十进制转二进制为例

int k;
//k进制转十进制
ll ktoD(string s)
{
    ll res=0,t=1;
    for(int i=s.size()-1;i>=0;i--)
    {
        if(s[i]>='0'&&s[i]<='9') res=res+(s[i]-'0')*t;
        else res=res+(s[i]-'A'+10)*t;
        
        t=t*k;
    }
    return res;
}
//十进制转k进制
string Dtok(ll n)
{
    string res="",tt="0123456789ABCDEF";
    ll x;
    while(n){
        x=n%k;
        res=tt[x]+res;
        n/=k;
    }
    if(res=="") res="0";
    return res;
}

二进制、八进制、十六进制互转

​ 二转八：取三合一 **二转十六：取四合一 ** 八转二：一分为三 十六转二：一分为四

​ 八转十六：八转二，再二转十六 十六转八：十六转二，再二转八

//八转二
string OtoB(string s)
{   
    // 存储0~7 八进制对应的 3位二进制
    string tt[8] = {"000","001","010","011","100","101","110","111"};
    string res; //res存放二进制答案
    // 8进制 ——> 2 进制：将每一位8进制转换为3位的2进制（通过数字对应数组直接获取！）然后拼接
    for(int i = 0; i < s.size(); i ++)
    {
        int x = s[i] - '0'; // 找到每一位8进制所对应的2进制表示
        res += tt[x]; // 拼接
    }
    // 清除前导0
    while(res[0] == '0' && res.size() > 1)//注：当8进制为000时，转成二进制后也为0，此时不能把000全部清除掉，要保留一个0！
    {
        res.erase(0, 1);
    }
    return res;
}
//二转十六
// 将4位的二进制转成10进制整数，再对应变为16进制符号：0~9 -> '0'~'9'; 10~15 -> 'A'~'F' 
char get_num(string s)
{
    ll res = 0, t = 1;
    // 从最低位按权展开，转换为10进制
    // 10进制在转为16进制
    for(int i = s.size() - 1; i >= 0; i --)
    {
        res = res + (s[i] - '0') * t;
        t = t * 2;
    }
    //10进制转16进制： 0~9 -> '0'~'9'; 10~15 -> 'A'~'F'
    char c; // 存放结果
    if(res < 10) c = res + '0';
    else c = res + 'A' - 10;
    return c;
}
string BtoH(string s)
{   
    string res=""; // 存放二进制
    // 看是否需要补零
    int len=s.size();
    if(len % 2 == 1) s = "000" + s;
    else if(len % 2 == 2) s = "00" + s;
    else if(len % 2 == 3) s = "0" + s;
    // 每每截取4位二进制数：substr(i, 4)截取字符串，i += 4
    for(int i = 0; i < len; i += 4)
    {
        string t;
        t = s.substr(i, 4);
        // 将4位二进制转换为16进制，输出
        res+=get_num(t);
    }
    return res;
}

//十六转二
string HtoB(string s)
{
    string tt[16]={"0000","0001","0010","0011","0100","0101","0110","0111","1000","1001","1010","1011","1100","1101","1110","1111"};
//求： 将每位16进制转为对应的4为二进制
//1. 将s[i]转换为0~15对应的整数，再求对应的4位2进制（技巧：通过数组下标获取对应二进制）
//2. 最终清除二进制字符串的前导0
    string res; // s存放16进制; res存放2进制答案
    for(int i = 0; i < s.size(); i ++)
    {
        //1. 将s[i]转换为0~15对应的整数
        int x;
        if(s[i] >= '0' && s[i] <= '9') x = s[i] - '0'; // 如果是0~9
        else x = s[i] - 'A' + 10;
        //1. 用字符串拼接16进制所对应表示的2进制
        res += tt[x];
    }
    //2. 最后清除前导0
    while(res[0] == '0' && res.size() > 1)//当16进制为0000时，转成二进制后也为0，此时不能把0000全部清除掉，要保留一个0！
    {
        res.erase(0,1);
    }
    return res;
}
//二转八
// 将3位的二进制(一定是0~7) 转成 10进制整数 对应的8进制必定也是：0 ~ 7
ll num(string s)
{
    ll t = 1, res = 0;
    // 从最低位按权展开，转换为10进制
    for(int i = s.size() - 1; i >= 0; i --)
    {
        res = res + (s[i] - '0') * t;
        t = t * 2;
    }
    return res;
}
string BtoO(string s)
{
    string res=""; // res存放答案
    // 看是否需要补0
    int len=s.size();
    if(len % 3 == 1) s = "00" + s;
    else if(len % 3 == 2) s = "0" + s;
    // 截取3位二进制，转为对应的八进制，输出
    for(int i = 0; i < len; i += 3)
    {
        string t;
        t = s.substr(i, 3);
        // 将每3位二进制转为八进制并输出
        res+=num(t)+'0';
    }
    return res;
}
//八转十六
string OtoH(string s)
{
    string res;
    res=OtoB(s);
    res=BtoH(res);
    return res;
}
//十六转八
string HtoO(string s)
{
    string res;
    res=HtoB(s);
    res=BtoO(res);
    return res;
}

2_SAT问题

2-SAT，简单的说就是给出n个集合，每个集合有两个元素，已知若干个 <a,b>，表示 a与 b矛盾（其中 a与 b属于不同的集合）。然后从每个集合选择一个元素，判断能否一共选 n个两两不矛盾的元素。显然可能有多种选择方案，一般题中只需要求出一种即可。

2-SAT问题可以转化为求解强连通分量的问题，并使用图论中的算法进行求解。

具体而言，可以通过构建一个有向图，其中每个变量对应两个节点（正面和否定），然后根据逻辑表达式构建有向边。

如果变量 x 在子句 (x OR y) 中出现，那么添加一条从 ~x 的节点到 y 的节点的有向边。

然后，对这个有向图进行强连通分量的计算，例如使用Tarjan算法。

如果在同一个强连通分量中存在一个变量及其否定，那么该2-SAT问题无解。

否则，对于每个强连通分量，选择一个节点并将其赋值为真，将它的否定节点赋值为假。

这样得到的变量赋值就是满足原始逻辑表达式的解。

struct TwoSat {
    int n;
    std::vector<std::vector<int>> e;
    std::vector<bool> ans;
    TwoSat(int n) : n(n), e(2 * n), ans(n) {}
    void addClause(int u, bool f, int v, bool g) {
        e[2 * u + !f].push_back(2 * v + g);
        e[2 * v + !g].push_back(2 * u + f);
    }
    bool satisfiable() {
        std::vector<int> id(2 * n, -1), dfn(2 * n, -1), low(2 * n, -1);
        std::vector<int> stk;
        int now = 0, cnt = 0;
        std::function<void(int)> tarjan = [&](int u) {
            stk.push_back(u);
            dfn[u] = low[u] = now++;
            for (auto v : e[u]) {
                if (dfn[v] == -1) {
                    tarjan(v);
                    low[u] = std::min(low[u], low[v]);
                } else if (id[v] == -1) {
                    low[u] = std::min(low[u], dfn[v]);
                }
            }
            if (dfn[u] == low[u]) {
                int v;
                do {
                    v = stk.back();
                    stk.pop_back();
                    id[v] = cnt;
                } while (v != u);
                ++cnt;
            }
        };
        for (int i = 0; i < 2 * n; ++i) if (dfn[i] == -1) tarjan(i);
        for (int i = 0; i < n; ++i) {
            if (id[2 * i] == id[2 * i + 1]) return false;
            ans[i] = id[2 * i] > id[2 * i + 1];
        }
        return true;
    }
    std::vector<bool> answer() { return ans; }
};